题目内容
已知函数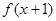 是定义在R上的奇函数,若对于任意给定的不等实数
是定义在R上的奇函数,若对于任意给定的不等实数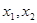 ,不等式
,不等式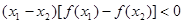 恒成立,则不等式
恒成立,则不等式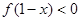 的解集为( )
的解集为( )
A.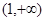 | B.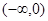 | C.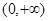 | D.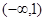 |
B
解析试题分析:由不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得,函数f(x)是定义在R上的减函数 ①.又因为函数f(x+1)是定义在R上的奇函数,所以有函数f(x+1)过点(0,0);故函数f(x)过点(1,0)②.①②相结合得:x>1时,f(x)<0.故不等式f(1-x)<0转化为1-x>1⇒x<0.选B.
考点:1.函数奇偶性;2.单调性

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
函数 的零点所在的一个区间是( )
的零点所在的一个区间是( )
A. | B. | C. | D.(1,2) |
函数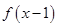 是
是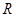 上的奇函数,
上的奇函数,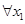 、
、 ,
,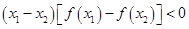 ,则
,则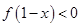 的解集是( )
的解集是( )
A.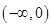 | B.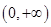 | C.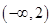 | D.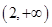 |
设 是
是 上的偶函数,且在
上的偶函数,且在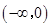 上为减函数,若
上为减函数,若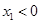 ,
,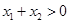 ,则( )
,则( )
A.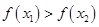 | B.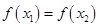 |
C.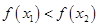 | D.不能确定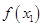 与 与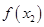 的大小 的大小 |
如果函数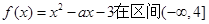 上单调递减,则实数
上单调递减,则实数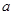 满足的条件是( )
满足的条件是( )
A.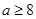 | B.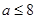 | C.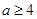 | D.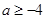 |
函数 的定义域为( )
的定义域为( )
A. | B.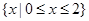 | C. 或 或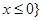 | D. |
已知定义在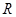 上的函数
上的函数 ,对任意
,对任意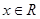 ,都有
,都有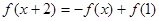 成立,若函数
成立,若函数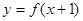 的图象关于点
的图象关于点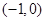 对称,则
对称,则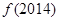 =( )
=( )
| A.0 | B.2014 | C.3 | D.—2014 |
若 、
、 是方程
是方程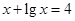 ,
,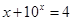 的解,函数
的解,函数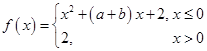 ,则关于
,则关于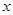 的方程
的方程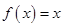 的解的个数是( )
的解的个数是( )
A.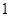 | B.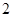 | C.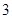 | D.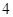 |
已知函数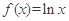 ,则函数
,则函数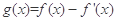 的零点所在的区间是( )
的零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |