题目内容
在△ABC中,若cos3A+cos3B+cos3C=1,求证:△ABC中必有一个内角为120°.
分析:根据三角形内角和,可知cos3A+cos3B+cos3C=(cos3A+cos3B)+cos[3π-3(A+B)],先正充分性,若A,B,C中有一个角是120°,不妨令A=120°,则可知B+C=60° 进而可知3A和3B 互补,进而可得cos3B+cos3C=0代入前边的等式可知cos3A+cos3B+cos3C=cos2π=1.进而看必要性,若cos3A+cos3B+cos3C=1进行恒等变换得到2cos
(cos
-cos
)=0,再进行等价转化即可得出结论.
| 3A+3B |
| 2 |
| 3A-3B |
| 2 |
| 3A+3B |
| 2 |
解答:解:∵A+B+C=π
∴cos3A+cos3B+cos3C
=(cos3A+cos3B)+cos[3π-3(A+B)]
(1)证充分性:若A,B,C中有一个角是120°,不妨令A=120°,
所以B+C=60°,所以3C+3B=180°,即3C和3B 互补
所以cos3B+cos3C=0
∴cos3A+cos3B+cos3C=cos2π=1
(2)证必要性
若cos3A+cos3B+cos3C=1
即cos3A+cos3B+cos(3π-3A-3B)=1
即cos3A+cos3B-cos(3A+3B)=1
即2cos
cos
-2cos2
+1=1
即2cos
(cos
-cos
)=0
即2cos
(-2sin
sin
)=0
∴cos
=0或sin
或sin
=0
又A,B,C是三角形的三个内角,故
<
,
<
,
<
,
∴
=
或
=π或
=π
∴A+B=
,即C=
或A=
或B=
∴A,B,C中必有一个是120°
综上知,命题成立.
∴cos3A+cos3B+cos3C
=(cos3A+cos3B)+cos[3π-3(A+B)]
(1)证充分性:若A,B,C中有一个角是120°,不妨令A=120°,
所以B+C=60°,所以3C+3B=180°,即3C和3B 互补
所以cos3B+cos3C=0
∴cos3A+cos3B+cos3C=cos2π=1
(2)证必要性
若cos3A+cos3B+cos3C=1
即cos3A+cos3B+cos(3π-3A-3B)=1
即cos3A+cos3B-cos(3A+3B)=1
即2cos
| 3A+3B |
| 2 |
| 3A-3B |
| 2 |
| 3A+3B |
| 2 |
即2cos
| 3A+3B |
| 2 |
| 3A-3B |
| 2 |
| 3A+3B |
| 2 |
即2cos
| 3A+3B |
| 2 |
| 3A |
| 2 |
| 3B |
| 2 |
∴cos
| 3A+3B |
| 2 |
| 3A |
| 2 |
| 3B |
| 2 |
又A,B,C是三角形的三个内角,故
| 3A+3B |
| 2 |
| 3π |
| 2 |
| 3A |
| 2 |
| 3π |
| 2 |
| 3B |
| 2 |
| 3π |
| 2 |
∴
| 3A+3B |
| 2 |
| π |
| 2 |
| 3A |
| 2 |
| 3B |
| 2 |
∴A+B=
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
∴A,B,C中必有一个是120°
综上知,命题成立.
点评:本题主要考查了同角三角函数关系,三角恒等变换的基本应用.解题的关键利用充分和必要两个方面去论证.

练习册系列答案
相关题目
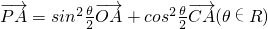 ,则
,则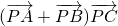 的最小值是________.
的最小值是________.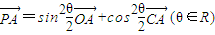 ,则
,则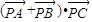 的最小值是 .
的最小值是 .