题目内容
 如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=
如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=
- A.1
- B.2
- C.

- D.随着P点的位置而定
B
分析:过点P作A′D′的垂线,交于点E,作A′B′的垂线,交于点F,连接A′P,然后表示出cosα,cosβ,cosγ,最后利用长方体的体对角线公式进行求解即可.
解答:过点P作A′D′的垂线,交于点E,作A′B′的垂线,交于点F,连接A′P
则cosα= ,cosβ=
,cosβ= ,cosγ=
,cosγ=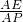
cos2α+cos2β+cos2γ=
=
=
=2
故选B
点评:本题主要考查了直线与平面所成的角,同时考查计算能力,属于中档题.
分析:过点P作A′D′的垂线,交于点E,作A′B′的垂线,交于点F,连接A′P,然后表示出cosα,cosβ,cosγ,最后利用长方体的体对角线公式进行求解即可.
解答:过点P作A′D′的垂线,交于点E,作A′B′的垂线,交于点F,连接A′P
则cosα=
 ,cosβ=
,cosβ= ,cosγ=
,cosγ=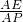
cos2α+cos2β+cos2γ=

=

=

=2
故选B
点评:本题主要考查了直线与平面所成的角,同时考查计算能力,属于中档题.

练习册系列答案
相关题目
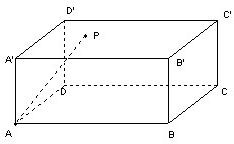 如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )
如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )| A、1 | ||
| B、2 | ||
C、
| ||
| D、随着P点的位置而定 |
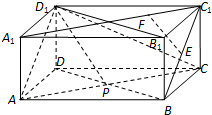 如图,在长方体ABCD-A1B1C1D1中,AB=AD=2.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=2. 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.