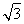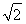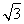题目内容
在平面斜坐标系xOy中∠xOy＝45°，点P的斜坐标定义为：若
＝x0e1＋y0e2(其中e1，e2分别为与斜坐标系的x轴，y轴同方向的单位向量)，则点P的坐标为(x0，y0)．若F1(－1，0)，F2(1，0)，且动点M(x，y)满足| 
|＝|
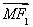|，则点M在斜坐标系中的轨迹方程为( )
A．x－
y＝0 B．x＋
y＝0 C.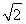 
x－y＝0 D. 
x＋y＝0
D
【解析】根据已知|e1|＝|e2|＝1，〈e1，e2〉＝45°，故e1·e2＝
，
＝－e1，
＝e1.设
＝xe1＋ye2，由|
|＝|
|，可得|
－
|＝|
－|，即|－(1＋x)e1－y e2|＝|(1－x)e1－y e2|，两端平方得(1＋x)2＋2(1＋x)y×＋y2＝(1－x)2－2(1－x)y×
＋y2，化简整理得
x＋y＝0.
练习册系列答案
相关题目
