题目内容
已知函数![]() 是定义域为R的偶函数,其图像均在x轴的上方,对任意的
是定义域为R的偶函数,其图像均在x轴的上方,对任意的![]() ,都有
,都有![]() ,且
,且![]() ,又当
,又当![]() 时,其导函数
时,其导函数![]() 恒成立。
恒成立。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)解关于x的不等式: ,其中
,其中![]()
(Ⅰ)![]()
![]()
(Ⅱ)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
解析:
(I)由![]() ,得:
,得:![]() 。
。
∵函数![]() 的图象均在x轴的上方,∴
的图象均在x轴的上方,∴![]() ∴
∴![]() ………1分
………1分
∵![]() ,又
,又![]() ,
,
∴![]() ,
,![]() ………4分
………4分
(II)
 又当
又当![]() 时,其导函数
时,其导函数![]() 恒成立,∴
恒成立,∴![]() 在区间
在区间![]() 上为单调递增函数………………………6分
上为单调递增函数………………………6分
∴![]() …………8分
…………8分
①当![]() 时,
时,![]() ;…………9分
;…………9分
②当![]() 时,
时,![]() ,∴
,∴![]() ;…10分
;…10分
③当![]() 时,
时,![]() ,∴
,∴![]() ……11分
……11分
综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。 ………12分
。 ………12分

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 是定义域为R的偶函数,且
是定义域为R的偶函数,且 ,若
,若 上是增函数,那么
上是增函数,那么 上是
上是 是定义域为R的偶函数,且
是定义域为R的偶函数,且 上是增函数,那么
上是增函数,那么 上是( )
上是( )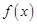 是定义域为R的偶函数,且
是定义域为R的偶函数,且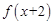 =
=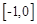 上是减函数,那么
上是减函数,那么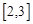 上是( )
上是( ) 是定义域为R的奇函数,当
是定义域为R的奇函数,当 时,
时, ,则
,则 等于
等于 B.
B.
 D.
D. 