题目内容
已知椭圆长轴的左右端点分别为A，B，短轴的上端点为M，O为椭圆的中心，F为椭圆的右焦点，且
·
＝1，｜
｜＝1．
（1）求椭圆的标准方程；
（2）若直线l交椭圆于P，Q两点，问：是否存在直线l，使得点F恰为△PQM的垂心?若存在，求出直线l的方程；若不存在，请说明理由．
解：（1）设椭圆方程为
，
所以
，又因为
，
所以
，则椭圆方程为
………………4分
（2）假设存在直线
符合题意。由题意可设直线方程为：
，代入得：
…………………6分
设
，则
…………………8分
解得：
或
……………………10分
当时，
三点共线，所以
所以
所以满足题意的直线存在，方程为：
……………………12分
练习册系列答案
优生乐园系列答案
相关题目
的一个焦点，已知椭圆长轴的两端点与F的距离分别为5和1，如果
在直线上
方，则k的取值范围是________．
·
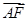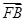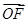＝1，｜
｜＝1．