题目内容
已知F1、F2是椭圆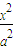
+
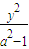=1的左右焦点，弦AB过F1，若△ABF2的周长为12，则椭圆的方程为 ．
【答案】分析：根据椭圆的定义，得出△ABF2的周长为（|AF1|+|AF2|）+（|BF1|+|BF2|）=4a，结合题意解出a=3，再代入题中的方程即可得到该椭圆的标准方程．
解答：解：∵椭圆的方程是
+
=1
，∴椭圆的焦点在x轴上
根据椭圆的定义，得|AF1|+|AF2|=|BF1|+|BF2|=2a，
∴△ABF2的周长为|AB|+|AF2|+|BF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=4a
结合题意△ABF2的周长为12，得4a=12，解之得a=3
将a=3代入椭圆方程，得
故答案为：
点评：本题给出椭圆经过左焦点的弦AB，在已知AB与右焦点构成的三角形周长情况下求椭圆的标准方程．着重考查了椭圆的定义与标准方程等知识，属于基础题．
解答：解：∵椭圆的方程是
+=1，∴椭圆的焦点在x轴上根据椭圆的定义，得|AF1|+|AF2|=|BF1|+|BF2|=2a，
∴△ABF2的周长为|AB|+|AF2|+|BF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=4a
结合题意△ABF2的周长为12，得4a=12，解之得a=3
将a=3代入椭圆方程，得
故答案为：
点评：本题给出椭圆经过左焦点的弦AB，在已知AB与右焦点构成的三角形周长情况下求椭圆的标准方程．着重考查了椭圆的定义与标准方程等知识，属于基础题．
练习册系列答案
习题精选系列答案
相关题目