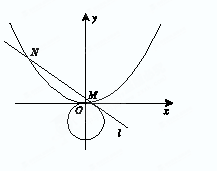
题目内容
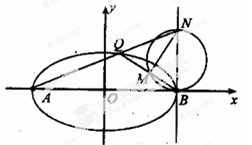
如图,在平面直角坐标系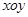 中,已知
中,已知 ,
,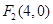 ,
,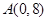 ,直线
,直线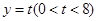 与线段
与线段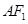 、
、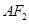 分别交于点
分别交于点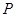 、
、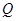 .
.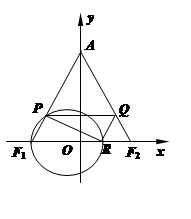
(1)当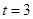 时,求以
时,求以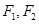 为焦点,且过
为焦点,且过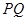 中点的椭圆的标准方程;
中点的椭圆的标准方程;
(2)过点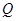 作直线
作直线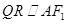 交
交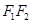 于点
于点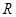 ,记
,记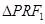 的外接圆为圆
的外接圆为圆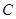 .
.
①求证:圆心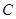 在定直线
在定直线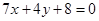 上;
上;
②圆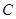 是否恒过异于点
是否恒过异于点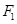 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由.
(1) (2)①略②
(2)①略② .
.
解析试题分析:(1)根据题意, ,
,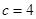 ,求出
,求出 ,可得到方程;(2)①解法一:根据题意写出
,可得到方程;(2)①解法一:根据题意写出 的坐标,线段
的坐标,线段 的中垂线的交点就是圆心,将圆心坐标代入
的中垂线的交点就是圆心,将圆心坐标代入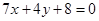 中,可得证;解法二:设出一般方程,将
中,可得证;解法二:设出一般方程,将 三点的坐标代入,联立求解;②根据①,写出圆系方程
三点的坐标代入,联立求解;②根据①,写出圆系方程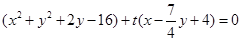 ,联立方程
,联立方程 解得该定点.
解得该定点.
试题解析:(1)设椭圆的方程为 ,
,
当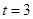 时,
时, 的中点为
的中点为 ,则
,则 1分
1分
而 ,所以
,所以 , 2分
, 2分
故椭圆的标准方程为 3分
3分
(Ⅱ)①解法一:易得直线 ,直线
,直线
可得 ,再由
,再由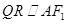 ,得
,得 5分
5分
则线段 的中垂线方程为
的中垂线方程为 , 6分
, 6分
线段 的中垂线方程为
的中垂线方程为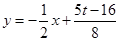 , 7分
, 7分
由 , 8分
, 8分
解得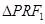 的外接圆的圆心坐标为
的外接圆的圆心坐标为 9分
9分
经验证,该圆心在定直线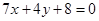 上 10分
上 10分
②由①可得圆C的方程为 11分
11分
该方程可整理为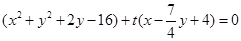 ,
,
则由 ,解得
,解得 或
或 , 13分
, 13分
所以圆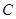 恒过异于点
恒过异于点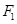 的一个定点,该点坐标为
的一个定点,该点坐标为 14分
14分
解法二: 易得直线 ,直线
,直线 5分
5分
所以可得 , 6分
, 6分
再由<

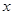 轴上,离心率
轴上,离心率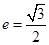 ,点
,点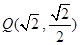 在椭圆C上.
在椭圆C上. 的标准方程;
的标准方程;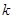
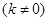 的直线
的直线 交椭圆
交椭圆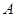 、
、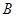 两点,且
两点,且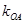 、
、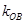 成等差数列,点M(1,1),求
成等差数列,点M(1,1),求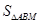 的最大值.
的最大值.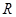 :
: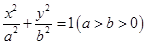 的长轴长为4,且过点
的长轴长为4,且过点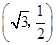 .
. 、
、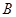 、
、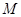 是椭圆上的三点,若
是椭圆上的三点,若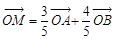 ,点
,点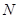 为线段
为线段 的中点,
的中点, 、
、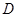 两点的坐标分别为
两点的坐标分别为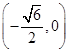 、
、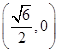 ,求证:
,求证: .
. 轴上,且过点
轴上,且过点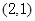 .
.
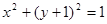 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点 若抛物线上一点
若抛物线上一点 满足
满足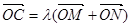
 ,求
,求 的取值范围.
的取值范围. .
.
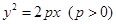 与直线
与直线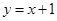 相切,
相切,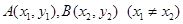 是抛物线上两个动点,
是抛物线上两个动点, 为抛物线的焦点,
为抛物线的焦点, 的垂直平分线
的垂直平分线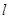 与
与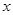 轴交于点
轴交于点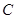 ,且
,且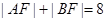 .
.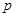 的值;
的值;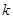 的取值范围.
的取值范围. 的参数方程为
的参数方程为 (t为参数,0<a<
(t为参数,0<a< ),曲线C的极坐标方程为
),曲线C的极坐标方程为 .
.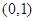 ,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.
,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.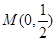 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为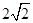 时,求直线m的方程.
时,求直线m的方程.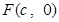 是椭圆
是椭圆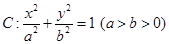 的右焦点,圆
的右焦点,圆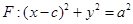 与
与 轴交于
轴交于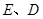 两点,
两点,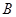 是椭圆
是椭圆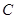 与圆
与圆 的一个交点,且
的一个交点,且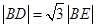 .
. 与
与 ,且
,且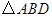 的面积等于
的面积等于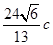 ,求椭圆
,求椭圆