题目内容
已知向量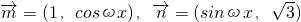 (ω>0),函数
(ω>0),函数 ,且f(x)图象上一个最高点的坐标为
,且f(x)图象上一个最高点的坐标为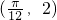 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为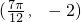 .
.
(1)求f(x)的解析式;
(2)在△ABC中,a,b,c是角A、B、C所对的边,且满足a2+c2-b2=ac,求角B的大
小以及f(A)的取值范围.
解:(1)∵向量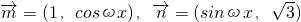
∴ =sinωx+
=sinωx+ cosωx=
cosωx= =
=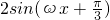 .--------------------------------------(2分)
.--------------------------------------(2分)
∵f(x)图象上一个最高点的坐标为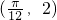 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为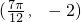 .
.
∴ ,
,
∴T=π,于是 .---------------(5分)
.---------------(5分)
所以 .---------------------------------(6分)
.---------------------------------(6分)
(2)∵a2+c2-b2=ac,∴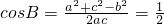 -----------------------------------7-分
-----------------------------------7-分
又0<B<π,∴ .
.
∴ --------------------------------------------(8分)
--------------------------------------------(8分)
∵ .于是
.于是 ,
,
∴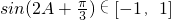 .------------------------------------------------------------(10分)
.------------------------------------------------------------(10分)
所以f(A)∈[-2,2].------------------------------------------------------------(12分)
分析:(1)由已知中向量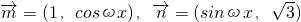 (ω>0),函数
(ω>0),函数 ,根据向量的数量积公式,结合辅助角公式,我们易将函数的解析式化为正弦型函数的形式,根据f(x)图象上一个最高点的坐标为
,根据向量的数量积公式,结合辅助角公式,我们易将函数的解析式化为正弦型函数的形式,根据f(x)图象上一个最高点的坐标为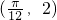 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为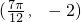 .我们求出函数的最值及周期,进而求出A,ω,φ值即可得到f(x)的解析式;
.我们求出函数的最值及周期,进而求出A,ω,φ值即可得到f(x)的解析式;
(2)又a2+c2-b2=ac由余弦定理及求出B的大小,进而根据三角形内角和为π确定A的范围,根据正弦函数的图象和性质即可求出f(A)的取值范围.
点评:本题考查的知识点是三角函数的最值,正弦型函数解析式的确定,余弦定理,其中(1)的关键是根据已知条件确定函数的最值及周期,进而求出A,ω,φ值,(2)的关键是根据已知的形式,选择使用余弦定理做为解答的突破口.
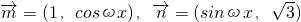
∴
 =sinωx+
=sinωx+ cosωx=
cosωx= =
=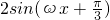 .--------------------------------------(2分)
.--------------------------------------(2分)∵f(x)图象上一个最高点的坐标为
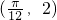 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为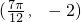 .
.∴
 ,
,∴T=π,于是
 .---------------(5分)
.---------------(5分)所以
 .---------------------------------(6分)
.---------------------------------(6分)(2)∵a2+c2-b2=ac,∴
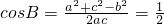 -----------------------------------7-分
-----------------------------------7-分又0<B<π,∴
 .
.∴
 --------------------------------------------(8分)
--------------------------------------------(8分)∵
 .于是
.于是 ,
,∴
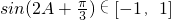 .------------------------------------------------------------(10分)
.------------------------------------------------------------(10分)所以f(A)∈[-2,2].------------------------------------------------------------(12分)
分析:(1)由已知中向量
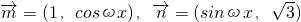 (ω>0),函数
(ω>0),函数 ,根据向量的数量积公式,结合辅助角公式,我们易将函数的解析式化为正弦型函数的形式,根据f(x)图象上一个最高点的坐标为
,根据向量的数量积公式,结合辅助角公式,我们易将函数的解析式化为正弦型函数的形式,根据f(x)图象上一个最高点的坐标为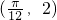 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为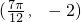 .我们求出函数的最值及周期,进而求出A,ω,φ值即可得到f(x)的解析式;
.我们求出函数的最值及周期,进而求出A,ω,φ值即可得到f(x)的解析式;(2)又a2+c2-b2=ac由余弦定理及求出B的大小,进而根据三角形内角和为π确定A的范围,根据正弦函数的图象和性质即可求出f(A)的取值范围.
点评:本题考查的知识点是三角函数的最值,正弦型函数解析式的确定,余弦定理,其中(1)的关键是根据已知条件确定函数的最值及周期,进而求出A,ω,φ值,(2)的关键是根据已知的形式,选择使用余弦定理做为解答的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目