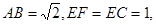题目内容
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1.
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求直线EC与平面ABED所成角的正弦值.
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求直线EC与平面ABED所成角的正弦值.


如图所示:
(1)由已知AB⊥平面ACD,DE⊥平面ACD,
∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥=
| 1 |
| 2 |
∴FH∥=AB,…3分
∴四边形ABFH是平行四边形,
∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,
∴BF∥平面ACD;…6分
(2)取AD中点G,连接CG、EG,则CG⊥AD,
又平面ABED⊥平面ACD,
∴CG⊥平面ABED,
∴∠CEG即为直线CE与平面ABED所成的角,…9分
设为α,则在Rt△CEG中,
有sinα=
| CG |
| CE |
| ||
2
|
| ||
| 4 |

练习册系列答案
相关题目
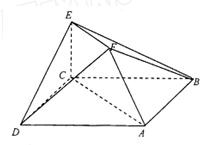 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=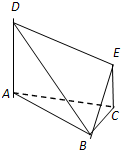 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=