题目内容
已知函数![]()
(Ⅰ)求![]() 的单调减区间
的单调减区间
(Ⅱ)若![]() 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
(Ⅰ)函数![]() 的单调递减区间为
的单调递减区间为![]()
(Ⅱ)函数![]() 在区间[-2,2]上的最小值为-7.
在区间[-2,2]上的最小值为-7.
解析:
(I)![]() 令
令![]() ,解得
,解得![]()
所以函数![]() 的单调递减区间为
的单调递减区间为![]()
(II)因为![]()
![]()
所以![]() 因为在(-1,3)上
因为在(-1,3)上![]() ,所以
,所以![]() 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于![]() 在[-2,-1]上单调递减,因此
在[-2,-1]上单调递减,因此![]() 和
和![]() 分别是
分别是![]() 在区间[-2,2]上的最大值和最小值.于是有
在区间[-2,2]上的最大值和最小值.于是有![]() ,解得
,解得![]()
故![]() 因此
因此![]()
即函数![]() 在区间[-2,2]上的最小值为-7.
在区间[-2,2]上的最小值为-7.

练习册系列答案
相关题目
 .
. 上的最大值和最小值.
上的最大值和最小值. .
. 成立的
成立的 的取值范围;
的取值范围; 时,求函数
时,求函数 的值域.
的值域. .
. 的单调区间;
的单调区间; 个单位得到函数
个单位得到函数 ,求
,求 在区间
在区间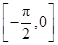 上的最小值和最大值.
上的最小值和最大值. .
. 的最小正周期及最值;
的最小正周期及最值; ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.