题目内容
【题目】已知函数
（
， 
）.
（1）当
时，讨论函数
的单调区间；
（2）当
时，若
对任意
恒成立，求
的取值范围.
【答案】（1）见解析；（2）
.
【解析】试题分析：（1）求导数，由导数大于0求增区间，导数小于0求减区间；
（2）讨论
和
三种情况，研究函数的单调性和最值即可.
试题解析：
（1）当
时， 
， 
，
①当
时， 
，所以函数
的单调递增区间为
；
②当
时，可知： 
，所以当
时， 
；
当
时， 
；
所以函数
的单调递增区间为
，递减区间为
.
（2）当
时， 
， 
，
若
，此时对任意
都有
， 
，
所以
恒成立；
下面考虑
时的情况：
若
，对任意
都有
， 
，所以
，所以
为
上的增函数，所以
，即
时满足题意；
若
，则由
， 
，可知：一定存在
，使得
，且当
时， 
，所以在
上， 
单调递减，从而有： 
时
，不满足题意.
综上可知， 
的取值范围为
.
练习册系列答案
小夫子全能检测系列答案
相关题目
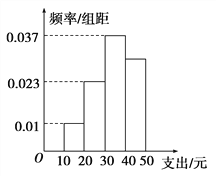
【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示：
组号 | 分组 | 频数 | 频率 |
第1组 |
|
| |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
|
（1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图（用阴影表示）；
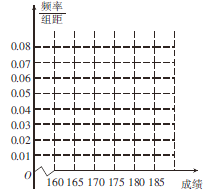
（2）为了能选拔出最优秀的选手，组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试，求第3、4、5组每组各抽取多少名选手进入第二轮面试；
（3）在（2）的前提下，组委会决定在5名选手中随机抽取2名选手接受
考官进行面试，求：第4组至少有一名选手被考官
面试的概率.
