Question

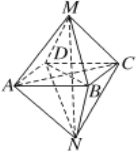
【题目】在棱长为的正方体中，分别是的中点，过三点的平面与正方体的下底面相交于直线；

（1）画出直线；

（2）设求的长；

（3）求D到的距离.

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）根据正方体的几何特征，连接DM并延长交D1A1的延长线于Q．连接NQ，即可得到满足条件的直线l；
（2）若l∩A1B1=P，即QN∩A1B1=P，易根据三角形全等的性质得到A1是QD1的中点．进而求出PB1的长；
（3）作D1H⊥l于H，连接DH，根据正方体的几何特征，易得DH⊥l，即DH的长就是D到l的距离．解Rt△QD1N即可得到答案．

(1)连结DM并延长交D1A1的延长线于Q,连结NQ，则NQ所在直线即为所求的直线．

(2)设QNA1B1=P,∵AM=A1M,∠AMD=∠A1MQ, ∠DAM=∠QA1M,易证得,所以,即A1是QD1的中点．

(3)作于H，连接，可证明，

则的长就是D到的距离.

在中，两直角边,斜边QN=．

所以 ，所以，

即D到的距离为．