题目内容
已知平面向量a=(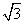 ,-1),b=
,-1),b=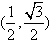 ,
,
(Ⅰ)若存在实数k和t,满足x=(t+2)a+(t2-t-5)b,y=-ka+4b且x⊥y,求出k关于t的关系式k=f(t);
(Ⅱ)根据(Ⅰ)的结论,试求出函数k=f(t)在t∈(-2,2)上的最小值。
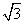 ,-1),b=
,-1),b=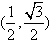 ,
,(Ⅰ)若存在实数k和t,满足x=(t+2)a+(t2-t-5)b,y=-ka+4b且x⊥y,求出k关于t的关系式k=f(t);
(Ⅱ)根据(Ⅰ)的结论,试求出函数k=f(t)在t∈(-2,2)上的最小值。
解:(Ⅰ)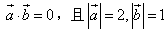 ,
,
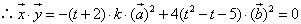 ,
,
∴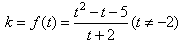 。
。
(Ⅱ)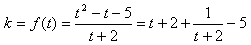 ,
,
∵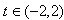 ,
,
∴t+2>0,
则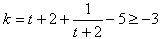 ,
,
当且仅当t+2=1,即t=-1时取等号,
∴k的最小值为-3。
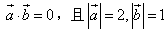 ,
,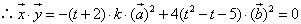 ,
,∴
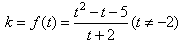 。
。(Ⅱ)
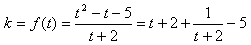 ,
,∵
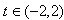 ,
,∴t+2>0,
则
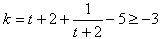 ,
,当且仅当t+2=1,即t=-1时取等号,
∴k的最小值为-3。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目