题目内容
(本小题满分18分)
定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
已知函数![]() ;
;![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的取值范围.
的取值范围.
(本小题满分18分)
[解]:(1)当![]() 时,
时,![]()
因为![]() 在
在![]() 上递减,所以
上递减,所以![]() ,即
,即![]() 在
在![]() 的值域为
的值域为![]()
故不存在常数![]() ,使
,使![]() 成立
成立
所以函数![]() 在
在![]() 上不是有界函数。 ……4分(没有判断过程,扣2分)
上不是有界函数。 ……4分(没有判断过程,扣2分)
(2)由题意知,![]() 在
在![]() 上恒成立。………5分
上恒成立。………5分
![]() ,
, ![]()
∴ ![]() 在
在![]() 上恒成立………6分
上恒成立………6分
∴ 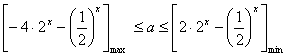 ………7分
………7分
设![]() ,
,![]() ,
,![]() ,由
,由![]()
![]() 得 t≥1,
得 t≥1,
设![]() ,
,![]()
![]()
所以![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,………9分(单调性不证,不扣分)
上递增,………9分(单调性不证,不扣分)
![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
, ![]() 在
在![]() 上的最小值为
上的最小值为![]()
所以实数![]() 的取值范围为
的取值范围为![]() 。…………………………………11分
。…………………………………11分
(3)![]() ,
,
∵ m>0 ,![]() ∴
∴ ![]() 在
在![]() 上递减,………12分
上递减,………12分
∴ ![]() 即
即![]() ………13分
………13分
①当![]() ,即
,即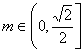 时,
时,![]() , ………14分
, ………14分
此时 ![]() ,………16分
,………16分
②当![]() ,即
,即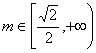 时,
时,![]() ,
,
此时 ![]() , ---------17分
, ---------17分
综上所述,当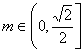 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
当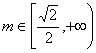 时,
时,![]() 的取值范围是
的取值范围是![]() ………18
………18

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成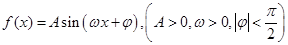 的图象的一部分如下图所示。
的图象的一部分如下图所示。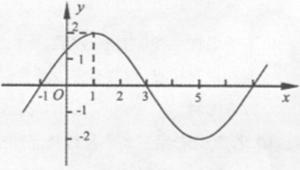
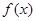 的解析式;
的解析式;
 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围;