题目内容
已知点P为△ABC所在平面上的一点，且
=
+t
，其中t为实数，若点P落在△ABC的内部，则t的取值范围是（ ）
| AP |
| 1 |
| 3 |
| AB |
| AC |
A、0＜t＜
| ||
B、0＜t＜
| ||
C、0＜t＜
| ||
D、0＜t＜
|
分析：用向量的加法法则将条件中的向量
，t
都用以A为起点的向量表示得到
=
+t
，画出图形，结合点P落在△ABC的内部从而得到选项．
| 1 |
| 3 |
| AB |
| AC |
| AP |
| 1 |
| 3 |
| AB |
| AC |
解答：
解：在AB上取一点D，使得
=
，
在AC上取一点E，使得：
=
．则由向量的加法的平行四边形法则得：
=
+
，
由图可知，若点P落在△ABC的内部，则0＜t＜
．
故选D．
解：在AB上取一点D，使得| AD |
| 1 |
| 3 |
| AB |
在AC上取一点E，使得：
| AE |
| 2 |
| 3 |
| AC |
| AP |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
由图可知，若点P落在△ABC的内部，则0＜t＜
| 2 |
| 3 |
故选D．
点评：本题考查向量的线性运算性质及几何意义，向量的基本运算，定比分点中定比的范围等等
练习册系列答案
相关题目
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
的解集是 ．
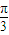），则|PQ|的最小值为 ．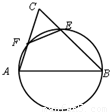
的解集是 ．
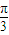），则|PQ|的最小值为 ．
，且AB = AC =
，BC =
，则异面直线PA与BC的距离是 。