题目内容
已知函数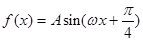 (其中
(其中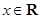 ,
,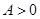 ,
,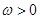 )的最大值为2,最小正周期为
)的最大值为2,最小正周期为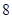 .
.
(1)求函数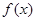 的解析式;
的解析式;
(2)若函数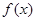 图象上的两点
图象上的两点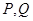 的横坐标依次为
的横坐标依次为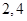 ,
,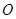 为坐标原点,求
为坐标原点,求
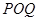 的值.
的值.
(1)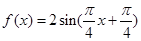 .
.
(2)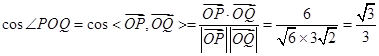 .
.
解析试题分析:(1)解:∵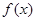 的最大值为2,且
的最大值为2,且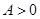 ,
,
∴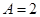 . 1分
. 1分
∵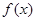 的最小正周期为
的最小正周期为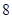 ,
,
∴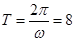 ,得
,得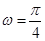 . 3分
. 3分
∴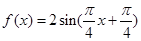 . 4分
. 4分
(2)解法1:∵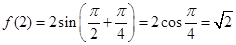 , 5分
, 5分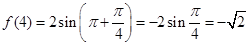 , 6分
, 6分
∴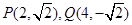 . 7分
. 7分
∴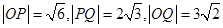 . 10分
. 10分
∴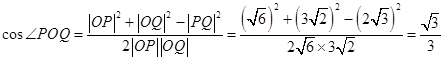 12分
12分
解法2:∵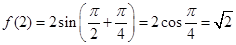 , 5分
, 5分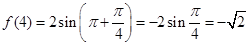 , 6分
, 6分
∴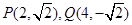 . 8分
. 8分
∴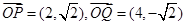 . 10分
. 10分
∴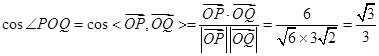 . 12分
. 12分
考点:本题主要考查平面向量的坐标运算,数量积、夹角计算,三角函数的性质。
点评:中档题,将平面向量与三角函数结合在一起进行考查,是高考题的一个显著特点。往往要利用三角公式化简函数,再研究函数的性质或利用函数的性质解题。求向量的夹角,是常见题目,应熟练掌握公式。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目






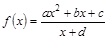 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.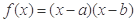 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
