题目内容
函数y=lg(sin x)+ 的定义域为 .函数y=
的定义域为 .函数y= Sin
Sin 的单调递增区间为 .
的单调递增区间为 .
【答案】分析:根据使函数有意义必须满足 ,再由正弦、余弦函数的性质得到x的范围,从而可确定函数的定义域.
,再由正弦、余弦函数的性质得到x的范围,从而可确定函数的定义域.
先将y= Sin
Sin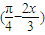 根据诱导公式化简为y=-
根据诱导公式化简为y=- sin(
sin(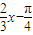 ),再求出y=
),再求出y= sin(
sin(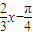 )的单调减区间,即可确定原函数的增区间.
)的单调减区间,即可确定原函数的增区间.
解答:解:①要使函数有意义必须有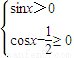 ,
,
即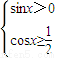 ,解得
,解得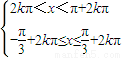
∴2kπ<x≤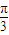 +2kπ,k∈Z,
+2kπ,k∈Z,
∴函数的定义域为{x|2kπ<x≤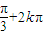 ,k∈Z}
,k∈Z}
②由y= Sin
Sin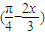 得y=-
得y=- sin(
sin(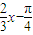 )
)
由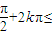
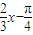
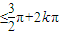
得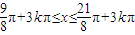
故函数的单调递增区间为:[ ]
]
故答案为:{x|2kπ<x≤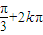 ,k∈Z};[
,k∈Z};[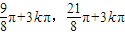 ].
].
点评:本题主要考查关于三角函数的定义域问题,考查复合函数的单调性问题.三角函数是高考的重点,每年必考且考查时一般以基础值为主,一定要强化基础题的练习.
 ,再由正弦、余弦函数的性质得到x的范围,从而可确定函数的定义域.
,再由正弦、余弦函数的性质得到x的范围,从而可确定函数的定义域.先将y=
 Sin
Sin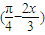 根据诱导公式化简为y=-
根据诱导公式化简为y=- sin(
sin(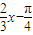 ),再求出y=
),再求出y= sin(
sin(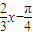 )的单调减区间,即可确定原函数的增区间.
)的单调减区间,即可确定原函数的增区间.解答:解:①要使函数有意义必须有
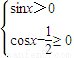 ,
,即
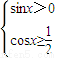 ,解得
,解得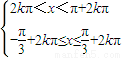
∴2kπ<x≤
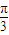 +2kπ,k∈Z,
+2kπ,k∈Z,∴函数的定义域为{x|2kπ<x≤
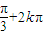 ,k∈Z}
,k∈Z}②由y=
 Sin
Sin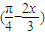 得y=-
得y=- sin(
sin(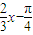 )
)由
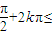
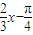
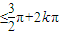
得
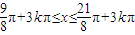
故函数的单调递增区间为:[
 ]
]故答案为:{x|2kπ<x≤
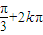 ,k∈Z};[
,k∈Z};[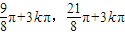 ].
].点评:本题主要考查关于三角函数的定义域问题,考查复合函数的单调性问题.三角函数是高考的重点,每年必考且考查时一般以基础值为主,一定要强化基础题的练习.

练习册系列答案
相关题目
 的定义域为 ________.函数y=
的定义域为 ________.函数y= Sin
Sin 的单调递增区间为 ________.
的单调递增区间为 ________.