题目内容
.(本题满分15分)已知二次函数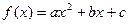 的图象经过点
的图象经过点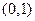 ,
,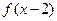 是偶函数,函数
是偶函数,函数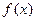 的图象与直线
的图象与直线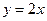 相切,且切点位于第一象限
相切,且切点位于第一象限
(Ⅰ)求函数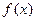 的解析式
的解析式
(Ⅱ)若对一切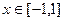 ,
, 不等式
不等式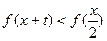 恒成立,求实数
恒成立,求实数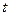 的取值范围
的取值范围
(Ⅲ)若关于x的方程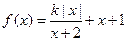 有三个不同的实数解,求实数k的值
有三个不同的实数解,求实数k的值
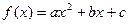 的图象经过点
的图象经过点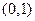 ,
,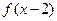 是偶函数,函数
是偶函数,函数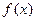 的图象与直线
的图象与直线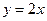 相切,且切点位于第一象限
相切,且切点位于第一象限(Ⅰ)求函数
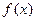 的解析式
的解析式(Ⅱ)若对一切
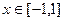 ,
, 不等式
不等式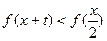 恒成立,求实数
恒成立,求实数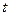 的取值范围
的取值范围(Ⅲ)若关于x的方程
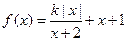 有三个不同的实数解,求实数k的值
有三个不同的实数解,求实数k的值
实数
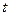 的取值范围是
的取值范围是 .
. (3)

.解(1)由题设知, . ①
. ①
令 ,解得
,解得 ,由题意可得
,由题意可得 ,即
,即 ,
,
所以 ,即
,即 . ②
. ②
由①、②可得 .
.
 又
又 恒成立,即
恒成立,即 恒成立,所以
恒成立,所以 ,且
,且 ,
,
即 ,所以
,所以 ,从而
,从而 .
.
因此函数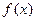 的解析式为
的解析式为  .
.
(2)由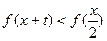 得
得 ,
,
整理得 .
.
当 即
即 时,
时, ,
,
此不等式对 一切
一切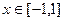 都成立的充要条件是
都成立的充要条件是 ,此不等式组无解. m
,此不等式组无解. m
当 即
即 时,
时, ,矛盾.
,矛盾.
当 即
即 时,
时, ,
,
此不等式对一切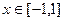 都成立的充要条件是
都成立的充要条件是 ,解得
,解得 .
.
综合可知,实数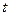 的取值范围是
的取值范围是 .
.
(3)
 . ①
. ①令
 ,解得
,解得 ,由题意可得
,由题意可得 ,即
,即 ,
,所以
 ,即
,即 . ②
. ②由①、②可得
 .
.  又
又 恒成立,即
恒成立,即 恒成立,所以
恒成立,所以 ,且
,且 ,
,即
 ,所以
,所以 ,从而
,从而 .
.因此函数
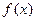 的解析式为
的解析式为  .
. (2)由
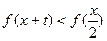 得
得 ,
,整理得
 .
.当
 即
即 时,
时, ,
,此不等式对
 一切
一切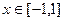 都成立的充要条件是
都成立的充要条件是 ,此不等式组无解. m
,此不等式组无解. m当
 即
即 时,
时, ,矛盾.
,矛盾. 当
 即
即 时,
时, ,
,此不等式对一切
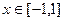 都成立的充要条件是
都成立的充要条件是 ,解得
,解得 .
.综合可知,实数
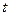 的取值范围是
的取值范围是 .
. (3)


练习册系列答案
相关题目
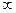 ,-4)
,-4) 上单调递增,试求a的取值范围。
上单调递增,试求a的取值范围。 (
( ∈R).
∈R).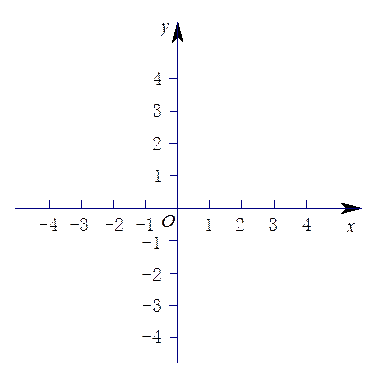
 ,若
,若 在区间
在区间 上的最大值
上的最大值 ,最小值
,最小值 ,设
,设
 的解析式;
的解析式;
 ,求
,求 的解析式;
的解析式;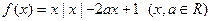 有下列四个结论:
有下列四个结论: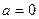 时,
时,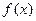 的图象关于原点对称
的图象关于原点对称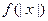 有最小值
有最小值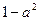
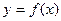 的图象与直线
的图象与直线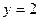 有两个不同交点,则
有两个不同交点,则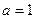
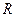 上是增函数,则
上是增函数,则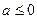

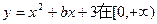 上是单调函数,则有 ( )
上是单调函数,则有 ( )



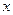 的方程
的方程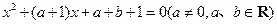 的两实根为
的两实根为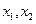 ,若
,若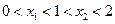 ,则
,则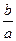 的取值范围是( )
的取值范围是( )


