题目内容
(本小题满分14分)
已知函数  ,
, .
.
(Ⅰ)当  时,求函数
时,求函数  的最小值;
的最小值;
(Ⅱ)当  时,讨论函数
时,讨论函数  的单调性;
的单调性;
(Ⅲ)求证:当  时,对任意的
时,对任意的  ,且
,且 ,有
,有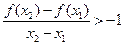 .
.
解:(Ⅰ)显然函数 的定义域为
的定义域为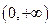 ,当
,当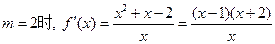 .
.
∴ 当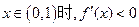 ,
,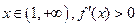 .
.
∴ 在
在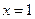 时取得最小值,其最小值为
时取得最小值,其最小值为 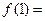
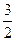 .----------------------------- 4分
.----------------------------- 4分
(Ⅱ)∵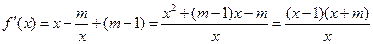 ,-----------5分
,-----------5分
∴(1)当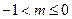 时,若
时,若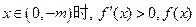 为增函数;
为增函数;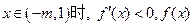 为减函数;
为减函数;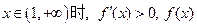 为增函数.
为增函数.
(2)当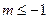 时,
时,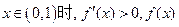 为增函数;
为增函数; 为减函数;
为减函数; 为增函数.------- 9分
为增函数.------- 9分
(Ⅲ)不妨设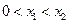 ,要证明
,要证明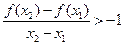 ,即证明:
,即证明: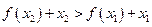
当 时,函数
时,函数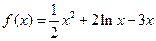 .
.
考查函数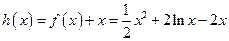 -------------------------------------------------10分
-------------------------------------------------10分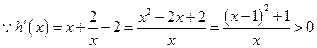
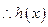 在
在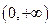 上是增函数,----------------------------------------------------12分
上是增函数,----------------------------------------------------12分
对任意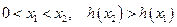 ,
,
所以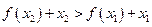 ,
,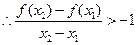 命题得证----------14分
命题得证----------14分
解析

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
(本小题满分12分) 为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第
为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第 小时教室内每立方米空气中的含药量为
小时教室内每立方米空气中的含药量为 毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为 (a为常数).函数图象如图所示.
(a为常数).函数图象如图所示.
根据图中提供的信息,解答下列问题:
(1)求从药物释放开始每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
|

 是定义在
是定义在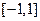 上的函数,且对任意
上的函数,且对任意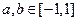 ,当
,当 时,都有
时,都有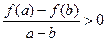 ;
;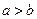 时,比较
时,比较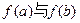 的大小;
的大小;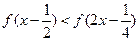 ;
;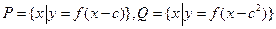 且
且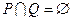 ,求
,求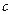 的取值范围。
的取值范围。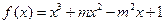 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.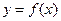 的切线,求此直线方程.
的切线,求此直线方程.
 解析式并判断
解析式并判断 当
当 时都有
时都有 成立,求满足条件
成立,求满足条件 的实数m的取值范围。
的实数m的取值范围。 为奇函数且
为奇函数且
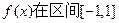 上是增函数。
上是增函数。 恒成立,求t的最小值。
恒成立,求t的最小值。