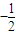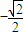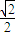Question

sin（x+27°）cos（18°-x）+sin（18°-x）cos（x+27°）=（　　）

• A、

  1

  2

• B、-

  1

  2

• C、-

  2

  2

• D、

  2

  2

Answer 1

分析：把x+27°看作α，18°-x看作β，则原式变为sinαcosβ+cosαsinβ，然后利用两角和的正弦函数公式及特殊角的三角函数值即可求出原式的值．

解答：解：原式=sin[（x+27°）+（18°-x）]=sin45°=

2

2

．
故选D

点评：此题考查学生灵活运用两角和与差的正弦函数公式及特殊角的三角函数值化简求值，是一道基础题．