题目内容
已知函数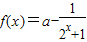 ,(x∈R).
,(x∈R).(Ⅰ)求证:不论a为何实数f(x)在(-∞,+∞)上为增函数;
(Ⅱ)若f(x)为奇函数,求a的值;
(Ⅲ)在(Ⅱ)的条件下,求f(x)在区间[1,5)上的最小值.
【答案】分析:(I)根据函数的单调性的定义进行判定,任取x1<x2,然后判定f(x1)-f(x2)的符号,从而得到结论;
(II)根据奇函数的定义建立等式关系,解之即可求出a的值;
(III)根据函数在R上单调递增,求出函数f(x)在区间[1,5)上的最小值即可.
解答:解:(Ⅰ)∵f(x)的定义域为R,任取x1<x2,
则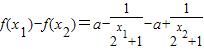 =
=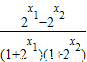 .
.
∵x1<x2,
∴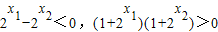 .
.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
所以不论a为何实数f(x)总为增函数.(4分)
(Ⅱ)∵f(x)在x∈R上为奇函数,
∴f(0)=0,即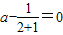 .
.
解得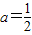 .(8分)
.(8分)
(Ⅲ)由(Ⅱ)知,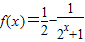 ,
,
由(Ⅰ) 知,f(x)为增函数,
∴f(x)在区间[1,5)上的最小值为f(1).
∵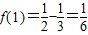 ,
,
∴f(x)在区间[1,5)上的最小值为 .(12分)
.(12分)
点评:本题主要考查了函数的单调性和奇偶性,以及函数的最值,属于中档题.
(II)根据奇函数的定义建立等式关系,解之即可求出a的值;
(III)根据函数在R上单调递增,求出函数f(x)在区间[1,5)上的最小值即可.
解答:解:(Ⅰ)∵f(x)的定义域为R,任取x1<x2,
则
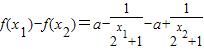 =
=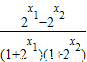 .
.∵x1<x2,
∴
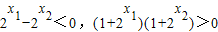 .
.∴f(x1)-f(x2)<0,即f(x1)<f(x2).
所以不论a为何实数f(x)总为增函数.(4分)
(Ⅱ)∵f(x)在x∈R上为奇函数,
∴f(0)=0,即
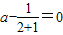 .
.解得
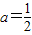 .(8分)
.(8分)(Ⅲ)由(Ⅱ)知,
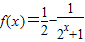 ,
,由(Ⅰ) 知,f(x)为增函数,
∴f(x)在区间[1,5)上的最小值为f(1).
∵
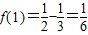 ,
,∴f(x)在区间[1,5)上的最小值为
 .(12分)
.(12分)点评:本题主要考查了函数的单调性和奇偶性,以及函数的最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围. (其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8.
(其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8. ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象 (x∈R,且x≠1),那么它的反函数为( )
(x∈R,且x≠1),那么它的反函数为( ) (x∈R,且x≠1)
(x∈R,且x≠1) (x∈R,且x≠6)
(x∈R,且x≠6) (x∈R,且x≠-
(x∈R,且x≠- )
)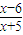 (x∈R,且x≠-5)
(x∈R,且x≠-5)