题目内容
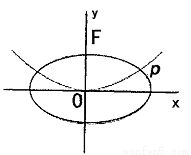
（本题满分14分）如图，抛物线
的焦点为F，椭圆
的离心率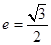
，C1与C2在第一象限的交点为
（1）求抛物线C1及椭圆C2的方程；
（2）已知直线
与椭圆C2交于不同两点A、B，点M满足
，直线FM的斜率为k1，试证明
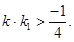
【答案】
（1）
（2）略
【解析】（1）将P(
，
)代入
得
抛物线C1的方程为
，焦点F(0，
)…………………………………2分
把P(，)代入
=l得
=l
又
解得
故椭圆C2的方程为…………………………………6分
（2）由
得
令
得
………………………………8分[来源:Zxxk.Com]
设
，
即点
为线段AB的中点，设
…………………………10分
…………………………11分
=
………………………12分
又
，
由
，即
.………………………14分
练习册系列答案
相关题目
，E是棱CC1上动点，F是AB中点，
；
、
的边长都是1，平面
平面
在
上移动，点
在
上移动，若
（
）
的长；
为何值时，
与面
所成锐二面角余弦值的大小.
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
平面C1CBB1；