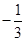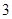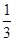题目内容
已知 在
在 处取得极值。
处取得极值。
(Ⅰ)证明: ;
;
(Ⅱ)是否存在实数 ,使得对任意
,使得对任意 ?若存在,求
?若存在,求 的所有值;若不存在,说明理由。
的所有值;若不存在,说明理由。
 在
在 处取得极值。
处取得极值。(Ⅰ)证明:
 ;
;(Ⅱ)是否存在实数
 ,使得对任意
,使得对任意 ?若存在,求
?若存在,求 的所有值;若不存在,说明理由。
的所有值;若不存在,说明理由。(Ⅰ)详见解析;(Ⅱ)存在唯一的实数a=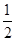 符合题意.
符合题意.
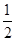 符合题意.
符合题意.试题分析:(Ⅰ)由已知条件得f¢(x0)=0得到关于x0的关系式,再求出f(x0);(Ⅱ)将原不等式转化为x2(lnx-a)+a≥0,考察关于x的函数g(x)=x2(lnx-a)+a的单调性,求出最小值g
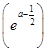 =a-
=a-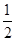 e2a-1,再研究关于a的函数h(a)=a-
e2a-1,再研究关于a的函数h(a)=a-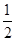 e2a-1,当a取哪些值时h(a)≥0.
e2a-1,当a取哪些值时h(a)≥0.试题解析:(Ⅰ)f¢(x)=
 .
.依题意,lnx0+x0+1=0,则lnx0=-(x0+1).
f(x0)=
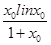 =
=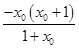 =-x0.
=-x0.(Ⅱ)f(x)≥
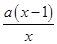 等价于x2(lnx-a)+a≥0.
等价于x2(lnx-a)+a≥0.设g(x)=x2(lnx-a)+a,则g¢(x)=x(2lnx-2a+1).
令g¢(x)=0,得x=
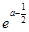 .
.当x∈
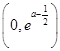 时,g¢(x)<0,g(x)单调递减;
时,g¢(x)<0,g(x)单调递减;当x∈
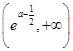 时,g¢(x)>0,g(x)单调递增.
时,g¢(x)>0,g(x)单调递增.所以g(x)≥g
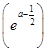 =a-
=a-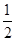 e2a-1.
e2a-1.于是f(x)≥
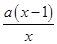 恒成立只需a-
恒成立只需a-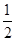 e2a-1≥0.
e2a-1≥0. 设h(a)=a-
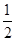 e2a-1,则h
e2a-1,则h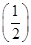 =0,
=0,且h¢(a)=1-e2a-1,h¢
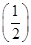 =0.
=0.当a∈(0,
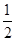 )时,h¢(a)>0,h(a)单调递增,h(a)<h
)时,h¢(a)>0,h(a)单调递增,h(a)<h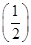 =0;
=0;当a∈(
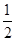 ,+∞)时,h¢(a)<0,g(x)单调递减,h(a)<h
,+∞)时,h¢(a)<0,g(x)单调递减,h(a)<h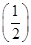 =0.
=0.因此,a-
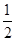 e2a-1≤0,当且仅当a=
e2a-1≤0,当且仅当a=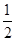 时取等号.
时取等号.综上,存在唯一的实数a=
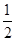 ,使得对任意x∈(0,+∞),f(x)≥
,使得对任意x∈(0,+∞),f(x)≥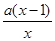 .
.
练习册系列答案
相关题目
 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数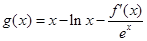 的最小值为1,其中
的最小值为1,其中 是函数f(x)的导数.
是函数f(x)的导数.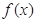 =
=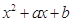 ,
,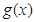 =
=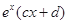 ,若曲线
,若曲线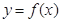 和曲线
和曲线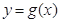 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线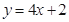 .
.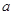 ,
,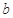 ,
,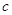 ,
,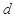 的值;
的值;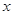 ≥-2时,
≥-2时,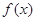 ≤
≤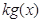 ,求
,求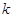 的取值范围.
的取值范围.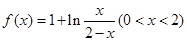 .
.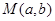 ,使得函数
,使得函数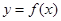 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数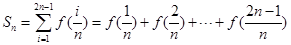 ,其中
,其中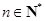 ,求
,求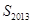 ;
;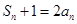 ,若不等式
,若不等式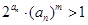 对
对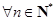 且
且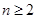 恒成立,求实数
恒成立,求实数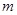 的取值范围.
的取值范围.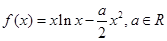
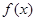 在(0,
在(0,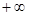 )单调递减,求a的最小值
)单调递减,求a的最小值 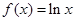 ,
,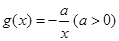
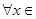 (0,e],都有f(x)≥g(x)+
(0,e],都有f(x)≥g(x)+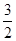 ,求实数a的取值范围.
,求实数a的取值范围.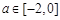 , 已知函数
, 已知函数
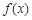 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增; 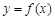 在点
在点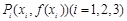 处的切线相互平行, 且
处的切线相互平行, 且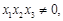 证明
证明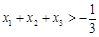 .
.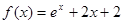 的零点所在区间是
的零点所在区间是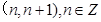 ,则
,则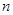 的值是______.
的值是______.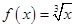 ,则
,则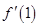 等于( )
等于( )