题目内容
(本小题12分)已知函数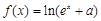 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求 的值;
的值;
(II)若 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求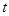 的取值范围;
的取值范围;
(Ⅲ)讨论关于 的方程
的方程 的根的个数.
的根的个数.
【答案】
∴ ,
,
(I) =0
=0
(II)
(Ⅲ)①当 时,方程无解.
时,方程无解.
②当 时,方程有一个根.
时,方程有一个根.
③当 时,方程有两个根.
时,方程有两个根.
【解析】解:(Ⅰ) 是奇函数,则
是奇函数,则 恒成立.
恒成立.
∴
即
∴
(II)由(I)知 ∴
∴
∴
又 在[-1,1]上单调递减,
在[-1,1]上单调递减,
∴
且 对
对 [-1,1]恒成立,
[-1,1]恒成立,
即 对
对 [-1,1]恒成立,
[-1,1]恒成立,
∴
∵ 在
在 上恒成立
上恒成立
∴
即 对
对 恒成立
恒成立
令 则
则
|
 ,
,
 .
.
(Ⅲ)由(I)知
令 ,
,
 ,
,
当 上为增函数;
上为增函数;
 上为减函数,
上为减函数,
当 时,
时, 而
而 ,
,
 、
、 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当 时,方程无解.
时,方程无解.
②当 时,方程有一个根.
时,方程有一个根.
③当 时,方程有两个根.
时,方程有两个根.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线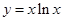
 处的切线方程。
处的切线方程。