题目内容
已知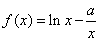
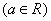 .
.
(Ⅰ)当 时,判断
时,判断 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若 在
在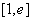 上的最小值为
上的最小值为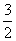 ,求
,求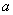 的值;
的值;
(III)若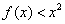 在
在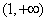 上恒成立,试求
上恒成立,试求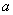 的取值范围.
的取值范围.
解:(Ⅰ) 的定义域为
的定义域为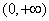
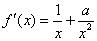 …………………………1分
…………………………1分
∵ ,
,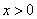
∴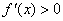 …………………………2分
…………………………2分
因此 在定义域
在定义域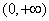 上为单调递增函数.…………………………3分
上为单调递增函数.…………………………3分
(Ⅱ)(1)令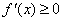 在
在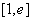 上恒成立,即
上恒成立,即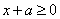
∴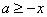 .
.
令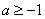 ,此时
,此时 在
在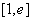 上为增函数.
上为增函数.
∴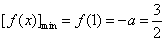 ,
,
得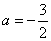 (舍去).…………………………5分
(舍去).…………………………5分
(2)令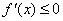 在
在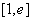 上恒成立,即
上恒成立,即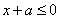
∴ .
.
令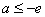 ,此时
,此时 在
在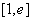 上为减函数.
上为减函数.
∴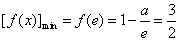 ,
,
得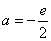 (舍去).…………………………7分
(舍去).…………………………7分
(3)当时,令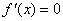 ,得
,得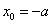 .
.
当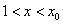 时,
时,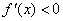 ,∴
,∴ 在
在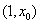 上为减函数.
上为减函数.
当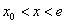 时,
时,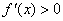 ,∴
,∴ 在
在 上为增函数.
上为增函数.
∴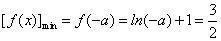
得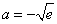 .…………………………9分
.…………………………9分
综上可知,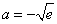 .…………………………10分
.…………………………10分
(III)由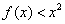 ,得
,得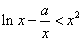 ,
,
∵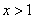 ,∴有
,∴有 ,
,
令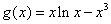 ,则
,则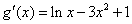 .…………………………12分
.…………………………12分
令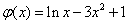 ,则
,则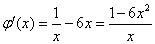 ,
,
∵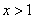 ,∴
,∴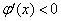 ,∴
,∴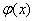 在
在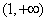 上单调递减,
上单调递减,
∴ ,
,
因此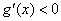 ,故
,故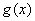 在
在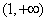 上单调递减,…………………………14分
上单调递减,…………………………14分
则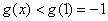 ,
,
∴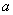 的取值范围是
的取值范围是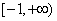 .
.

练习册系列答案
相关题目
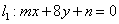 和
和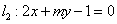 ,试确定
,试确定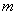 ,
,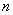 的值,使(1)
的值,使(1)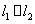 ;(2)
;(2)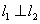 ,且
,且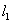 在
在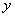 轴上的截距为-1.
轴上的截距为-1. ,A的角平分线AD=
,A的角平分线AD= ,则AC= .
,则AC= .  ,
, ,
, ,…,若
,…,若 ,
, 则( )
则( ) B.
B. C.
C. D.
D.
 的定义域为集合
的定义域为集合 ,函数
,函数 的值域为集合
的值域为集合 .
. :
: ,命题
,命题 :
: ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的展开式中,
的展开式中, 的系数为 ( )
的系数为 ( ) 120 B 120 C
120 B 120 C  上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为( ).
的解集为( ).  B.
B.
 D.
D.

 ,求函数
,求函数 的最小正周期及图像的对称轴方程;
的最小正周期及图像的对称轴方程; ,
, ,求实数
,求实数 的值。
的值。