题目内容
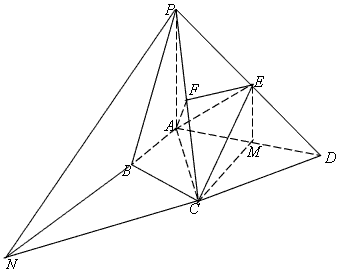
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,
(1)求证:PC⊥AE;
(2)求证:CE∥平面PAB;
(3)求三棱锥P-ACE的体积V。
(1)求证:PC⊥AE;
(2)求证:CE∥平面PAB;
(3)求三棱锥P-ACE的体积V。
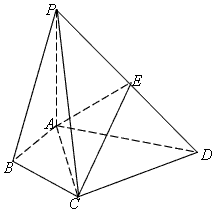
| 解:(1)在Rt△ABC中,AB=1,∠BAC=60°, ∴BC=  ,AC=2, ,AC=2,取PC中点F,连AF,EF, ∵PA=AC=2, ∴PC⊥AF, ∵PA⊥平面ABCD, 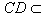 平面ABCD, 平面ABCD,∴PA⊥CD, 又∠ACD=90°,即CD⊥AC, ∴CD⊥平面PAC, ∴CD⊥PC, ∴EF⊥PC, ∴PC⊥平面AEF, ∴PC⊥AE; (2)取AD中点M,连EM,CM, 则EM∥PA, ∵EM  平面PAB,PA 平面PAB,PA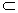 平面PAB, 平面PAB, ∴EM∥平面PAB, 在Rt△ACD中,∠CAD=60°,AC=AM=2, ∴∠ACM=60°,而∠BAC=60°, ∴MC∥AB, ∵MC 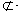 平面PAB,AB 平面PAB,AB 平面PAB, 平面PAB, ∴MC∥平面PAB, ∵EM∩MC=M, ∴平面EMC∥平面PAB, ∵EC  平面EMC, 平面EMC,∴EC∥平面PAB。 (3)由(1)知AC=2,EF= 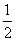 CD,且EF⊥平面PAC, CD,且EF⊥平面PAC,在Rt△ACD中,AC=2,∠CAD=60°, ∴CD=2 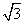 ,得EF= ,得EF=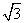 , ,则V= 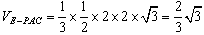 。 。 |
 |

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,