题目内容
(本小题满分13分)已知幂函数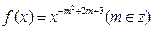 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数.
上是单调增函数.
(Ⅰ)求函数
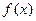 的解析式;
的解析式;
(Ⅱ)设函数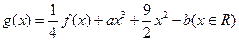 ,其中
,其中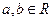 .若函数
.若函数 仅在
仅在
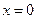 处有极值,求
处有极值,求 的取值范围.
的取值范围.
(1)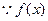 在区间
在区间 上是单调增函数,
上是单调增函数,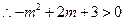 即
即
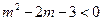
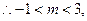 又
又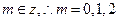 ………………………3分
………………………3分
而 时,
时,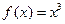 不是偶函
不是偶函 数,
数,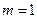 时,
时,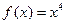 是偶函数,
是偶函数,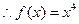 .………………………6分
.………………………6分
(2)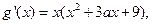 显然
显然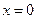 不是方程
不是方程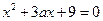 的根. ………………………8分
的根. ………………………8分
为使 仅在
仅在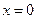 处有极值,必须
处有极值,必须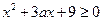 恒成立,
恒成立,
即有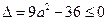 ,解不等式,得
,解不等式,得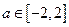 .
.
这时, 是唯一极值.
是唯一极值. 
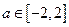 .………………………13分
.………………………13分
解析

练习册系列答案
相关题目
 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知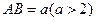 ,
,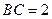 ,且
,且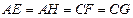 ,设
,设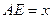 ,绿地面积为
,绿地面积为 .
.
1、写出 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
2、当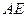 为何值时,绿地面积
为何值时,绿地面积 最大?
最大?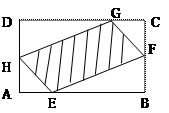
已知函数f(x)是偶函数,在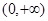 上导数
上导数 >0恒成立,则下列不等式成立的是( ).
>0恒成立,则下列不等式成立的是( ).
| A.f(-3)<f(-1)<f(2) | B.f(-1)<f(2)<f(-3) |
| C.f(2)<f(-3)<f(-1) | D.f(2)<f(-1)<f(-3) |
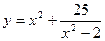 (
(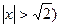 的最小值以及相应的
的最小值以及相应的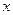 的值;
的值;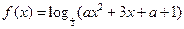
 时,求函数
时,求函数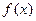 的定义域、值域及单调区间;
的定义域、值域及单调区间; ,不等式
,不等式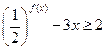 恒成立,求正实
恒成立,求正实 数
数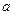 的取值范围.
的取值范围. =x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式.
=x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式. 况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:
况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明: 当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式.
当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式. =
= +
+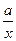 有如下性质:如果常数
有如下性质:如果常数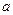 >0,那么该
>0,那么该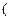 0,
0,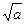
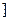 上是减函数,在
上是减函数,在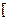
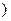 上是增函数.
上是增函数.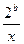 (
(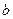 的值;
的值;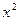 +
+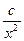 (常数
(常数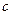 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;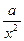 (常数
(常数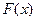 =
=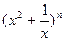 +
+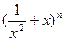 (
(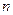 是正整数)在区间[
是正整数)在区间[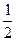 ,2]上的最大值和最小值(可利用你
,2]上的最大值和最小值(可利用你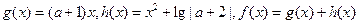 ,其中
,其中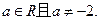
 为偶函数,求a的值;
为偶函数,求a的值;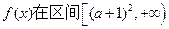 上是增函数,命题q:函数
上是增函数,命题q:函数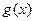 是减函数,如果p或q为真,p且q为假,求a的取值范围。
是减函数,如果p或q为真,p且q为假,求a的取值范围。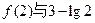 的大小。
的大小。