Question

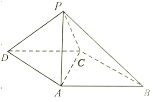
【题目】如图，在四棱锥中，底面为平行四边形，点在面内的射影为，，点到平面的距离为，且直线与垂直．

（Ⅰ）在棱上找一点，使直线与平面平行，并说明理由；

（Ⅱ）在（Ⅰ）的条件下，求二面角的大小．

Answer 1

【答案】（Ⅰ）点为中点时直线与平面平行，证明详见解析；（Ⅱ）．

【解析】

（Ⅰ）点为中点时，连接，交于点，可得，从而得线面平行；

（Ⅱ）取中点，连接，利用已知垂直可证平面，从而有，，得二面角的平面角为，它与互补，结论可得．

（Ⅰ）点为中点时直线与平面平行，

证明：连接，交于点，则点为的中点，因为点为中点，

故为的中位线，则，平面，平面，所以与平面平行．

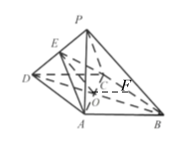
（Ⅱ）根据题意，底面，底面，则有，

，所以平面，

由（Ⅰ）可知，又，所以，

平面，平面，所以，

取中点，连接，由于是中点，则，，

∴为二面角的平面角，其为钝角，

那么，所成的角即为二面角的补角，

等腰直角中，，

因此二面角的大小为．