题目内容
已知函数![]() .
.
(1)当![]() 时
时![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围.
的取值范围.
(2)是否存在这样的实数![]() 使得函数
使得函数![]() 在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出
在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
⑴(0,1)∪(1,![]() );⑵不存在。
);⑵不存在。
解析:
解:(1)由假设,![]() >0,对一切
>0,对一切![]() 恒成立,
恒成立,![]()
显然,函数g(x)= ![]() 在[0,2]上为减函数,从而g(2)=
在[0,2]上为减函数,从而g(2)=![]() >0得到
>0得到![]() <
<![]()
∴![]() 的取值范围是(0,1)∪(1,
的取值范围是(0,1)∪(1,![]() )
)
(2)假设存在这样的实数![]() ,由题设知
,由题设知![]() ,即
,即![]() =1
=1
∴![]() =
=![]() 此时
此时![]()
当![]() 时,
时,![]() 没有意义,故这样的实数不存在.
没有意义,故这样的实数不存在.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 ,
,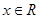 .
.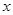 为何值时,
为何值时,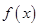 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,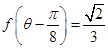 ,求
,求 的值.
的值.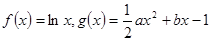 ,
, 且
且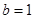 时,证明:对
时,证明:对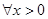 ,
,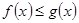 ;
;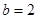 ,且
,且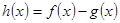 存在单调递减区间,求
存在单调递减区间,求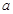 的取值范围;
的取值范围;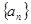 ,若存在常数
,若存在常数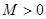 ,
,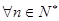 ,都有
,都有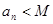 ,则称数列
,则称数列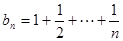 ,试判断数列
,试判断数列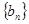 是否有上界.
是否有上界.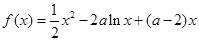 ,
,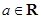 .
.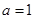 时,求函数
时,求函数 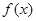 的最小值;
的最小值; 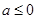 时,讨论函数
时,讨论函数 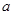 ,对任意的
,对任意的
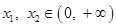 ,且
,且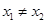 ,有
,有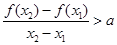 ,恒成立,若存在求出
,恒成立,若存在求出