题目内容
(2009湖南卷理)(本小题满分13分)
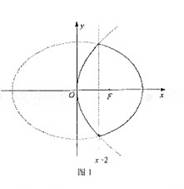
在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标与18之和 ![]()
![]()
(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线I与轨迹C相交于M,N两点,求线段MN长度的最大值。
解析:(Ⅰ)设点P的坐标为(x,y),则![]() 3x-2
3x-2
由题设
当x>2时,由①得![]()
化简得 ![]()
当![]() 时 由①得
时 由①得![]()
化简得![]()
故点P的轨迹C是椭圆![]() 在直线x=2的右侧部分与抛物线
在直线x=2的右侧部分与抛物线![]() 在直线x=2的左侧部分(包括它与直线x=2的交点)所组成的曲线,参见图1
在直线x=2的左侧部分(包括它与直线x=2的交点)所组成的曲线,参见图1
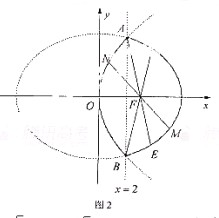
(Ⅱ)如图2所示,易知直线x=2与![]() ,
,![]() 的交点都是A(2,
的交点都是A(2,![]() ),
),
B(2,![]() ),直线AF,BF的斜率分别为
),直线AF,BF的斜率分别为![]() =
=![]() ,
,![]() =
=![]() .
.
当点P在![]() 上时,由②知
上时,由②知
![]() . ④
. ④
当点P在![]() 上时,由③知
上时,由③知 ![]()
![]()
![]() ⑤
⑤
若直线l的斜率k存在,则直线l的方程为![]()
(i)当k≤![]() ,或k≥
,或k≥![]() ,即k≤-2
,即k≤-2 ![]() 时,直线I与轨迹C的两个交点M(
时,直线I与轨迹C的两个交点M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )都在C
)都在C ![]() 上,此时由④知
上,此时由④知
MF= 6 - ![]()
![]() NF= 6 -
NF= 6 - ![]()
![]()
![]()
![]()
从而MN= MF+ NF= (6 - ![]()
![]() )+ (6 -
)+ (6 - ![]()
![]() )=12 -
)=12 - ![]() (
( ![]() +
+![]() )
)
由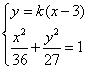 得
得![]() 则
则![]() ,
,![]() 是这个方程的两根,所以
是这个方程的两根,所以![]() +
+![]() =
=![]() *MN=12 -
*MN=12 - ![]() (
(![]() +
+![]() )=12 -
)=12 - ![]()
因为当![]()
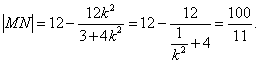
![]()
![]()
当且仅当![]() 时,等号成立。
时,等号成立。
(2)当![]() 时,直线L与轨迹C的两个交点
时,直线L与轨迹C的两个交点![]() 分别在
分别在![]() 上,不妨设点
上,不妨设点![]() 在
在![]() 上,点
上,点![]() 上,则④⑤知,
上,则④⑤知,![]()
设直线AF与椭圆![]() 的另一交点为E
的另一交点为E![]()
![]()
所以![]() 。而点A,E都在
。而点A,E都在![]() 上,且
上,且
![]() 有(1)知
有(1)知![]()
![]()
![]()
若直线![]() 的斜率不存在,则
的斜率不存在,则![]() =
=![]() =3,此时
=3,此时
![]()
综上所述,线段MN长度的最大值为![]()

 智能训练练测考系列答案
智能训练练测考系列答案