题目内容
（1）已知α，β都是锐角，sinα=
，cos（α+β）=
，求sinβ的值．
（2）若α，β都是锐角，sinα=
，sinβ=
，求α+β的值．
| 3 |
| 5 |
| 5 |
| 13 |
（2）若α，β都是锐角，sinα=
| ||
| 5 |
| ||
| 10 |
（1）∵α，β都是锐角，∴α+β∈（0，π），
又sinα=
，cos（α+β）=
，
∴cosα=
，sin（α+β）=
，
则sinβ=sin[（α+β）-α]
=sin（α+β）cosα-cos（α+β）sinα
=
×
-
×
=
．
（2）：∵α、β为锐角，sinα=
，sinβ=
，
∴cosα=
=
cosβ=
=
∴cos（α+β）=cosαcosβ-sinαsinβ=
，
α、β为锐角．
∴α+β=
又sinα=
| 3 |
| 5 |
| 5 |
| 13 |
∴cosα=
| 4 |
| 5 |
| 12 |
| 13 |
则sinβ=sin[（α+β）-α]
=sin（α+β）cosα-cos（α+β）sinα
=
| 12 |
| 13 |
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 33 |
| 65 |
（2）：∵α、β为锐角，sinα=
| ||
| 5 |
| ||
| 10 |
∴cosα=
| 1-sin2α |
2
| ||
| 5 |
cosβ=
| 1-sin2β |
3
| ||
| 10 |
∴cos（α+β）=cosαcosβ-sinαsinβ=
| ||
| 2 |
α、β为锐角．
∴α+β=
| π |
| 4 |
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
．
．
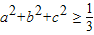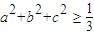