题目内容
若函数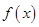 满足:
满足: ,则
,则 的最小值为( )
的最小值为( )
A.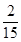 | B.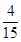 | C.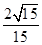 | D.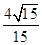 |
B
解析试题分析:根据 ①,有
①,有 ②,由①②联立,消去
②,由①②联立,消去 得
得 ,当
,当 ;当
;当 ,所以
,所以 .
.
考点:方程组思想求函数解析式;均值不等式;

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
若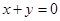 ,则
,则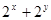 的最小值是( )
的最小值是( )
A.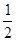 | B.1 | C.2 | D.4 |
若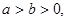 则下列不等式成立的是 ( )
则下列不等式成立的是 ( )
A. | B.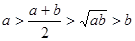 |
C.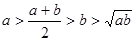 | D.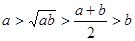 |
已知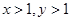 ,且
,且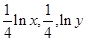 ,成等比数列,则xy( )
,成等比数列,则xy( )
| A.有最大值e | B.有最大值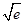 | C.有最小值e | D.有最小值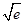 |
设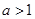 ,
,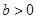 ,若
,若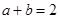 ,则
,则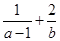 的最小值为( )
的最小值为( )
A.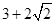 | B.6 | C.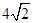 | D.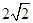 |
设第一象限内的点 满足约束条件
满足约束条件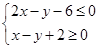 ,若目标函数
,若目标函数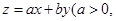
 的最大值为40,则
的最大值为40,则 的最小值为( )
的最小值为( )
A. | B. | C.1 | D.4 |
已知关于x的不等式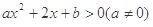 的解集是
的解集是 ,且a>b,则
,且a>b,则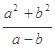 的最小值是( )
的最小值是( )
A.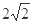 | B.2 | C.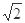 | D.1 |
若x≥0,y≥0且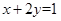 ,那么2x+3y2的最小值为( )
,那么2x+3y2的最小值为( )
| A.2 |
B.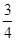 |
C.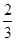 |
| D.0 |
 取得最大值时,x+2y-z的最大值为( )
取得最大值时,x+2y-z的最大值为( )
