题目内容
设函数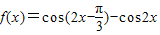 ,x∈R.
,x∈R.(Ⅰ)求f(x)在
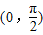 上的值域;
上的值域;(Ⅱ)记△ABC的内角A,B,C的对边长分别为a,b,c,若
 ,求c的值.
,求c的值.
【答案】分析:(I) 利用两角和差的三角公式化简函数的解析式,根据角的范围及函数的单调性求出函数的值域.
(II)由 f(A)=1 求得 ,根据
,根据 求出A=
求出A= ,利用余弦定理求出c的值.
,利用余弦定理求出c的值.
解答:解:(I) =
=
= =
= .∵
.∵ ,∴
,∴ ,
,
∴ ,即f(x)在
,即f(x)在 的值域为
的值域为 .
.
(II)由(I)可知, ,∴
,∴ .
.
∵0<A<π,∴ ,∴
,∴ .
.
∵a2=b2+c2-2bccosA,把 代入,得到c2-3c+2=0,∴c=1或c=2.
代入,得到c2-3c+2=0,∴c=1或c=2.
点评:本题考查两角和差的三角公式的应用,余弦定理,以及正弦函数的值域,求出角A的大小是解题的关键.
(II)由 f(A)=1 求得
 ,根据
,根据 求出A=
求出A= ,利用余弦定理求出c的值.
,利用余弦定理求出c的值.解答:解:(I)
 =
=
=
 =
= .∵
.∵ ,∴
,∴ ,
,∴
 ,即f(x)在
,即f(x)在 的值域为
的值域为 .
.(II)由(I)可知,
 ,∴
,∴ .
.∵0<A<π,∴
 ,∴
,∴ .
.∵a2=b2+c2-2bccosA,把
 代入,得到c2-3c+2=0,∴c=1或c=2.
代入,得到c2-3c+2=0,∴c=1或c=2.点评:本题考查两角和差的三角公式的应用,余弦定理,以及正弦函数的值域,求出角A的大小是解题的关键.

练习册系列答案
相关题目
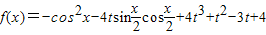 ,x∈R,其中|t|≤1,将f(x)的最小值记为g(t).
,x∈R,其中|t|≤1,将f(x)的最小值记为g(t).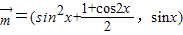 ,
,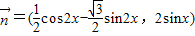 ,设函数
,设函数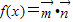 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
,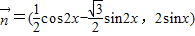 ,设函数
,设函数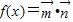 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域.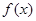 (x∈R)为奇函数,
(x∈R)为奇函数, =
= ,
, ,则
,则 =(
)
=(
)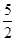 D.5
D.5