Question

【题目】若函数，ω＞0，|φ|＜）的一个零点与之相邻的对称轴之间的距离为，且时f（x）有最小值．

（1）求的解析式；

（2）若，求f（x）的值域．

Answer 1

【答案】(1) f（x）=cos（2x-）;(2) .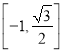

【解析】试题分析：（1）由条件得四分之一周期，解得ω，代入（），并根据|φ|＜解得（2）由，根据余弦函数性质可得f（x）的值域．

试题解析：（1）∵函数f（x）的一个零点与之相邻的对称轴之间的距离为，

∴f（x）的周期T=π，即，∴ω=2．又∵x=时f（x）有最小值，

∴f（）=cos（+φ）=-1，∴+φ=2kπ+π，解得φ=2kπ-，

∵|φ|＜，∴φ=-，∴f（x）=cos（2x-）．

（2）∵x∈[，]，∴，

∴当2x-=π时，f（x）取得最小值-1，当2x-=时，f（x）取得最大值，

∴f（x）的值域是[-1，]．