Question

【题目】如图：PA⊥平面ABCD，ABCD是矩形,PA=AB=1，AD=，点F是PB的中点，点E在边BC上移动.

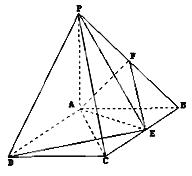
（1）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；

（2）证明：无论点E在边BC的何处，都有PE⊥AF.

Answer 1

【答案】（1）见解析；（2）见解析。

【解析】试题分析：；（1）利用三角形的中位线及线面平行的判定定理解决；
（2）∵PA⊥平面ABCD，∴EB⊥PA又EB⊥AB，∴EB⊥平面PAB，又AF平面PAB，
∴AF⊥BE．又PA=AB=1，点F是PB的中点，∴AF⊥PB，所以可证出AF⊥平面PBE 则AF⊥PE易证得．

试题解析：

（1）当点E为BC的中点时，EF与平面PAC平行．
∵在△PBC中，E、F分别为BC、PB的中点，
∴EF∥PC，又EF平面PAC，而PC平面PAC，
∴EF∥平面PAC．
（2）证明：
∵PA⊥平面ABCD，BE平面ABCD，
∴EB⊥PA，又EB⊥AB，AB∩AP=A，AB，AP平面PAB，
∴EB⊥平面PAB，又AF平面PAB，
∴AF⊥BE．
又PA=AB=1，点F是PB的中点，
∴AF⊥PB，
又∵PB∩BE=B，PB，BE平面PBE，
∴AF⊥平面PBE．
∵PE平面PBE，
∴AF⊥PE．