题目内容
关于函数f(x)=4sin(2x+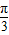 )(x∈R),有下列命题:
)(x∈R),有下列命题:①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y=4cos(2x-
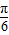 );
);③y=f(x)的图象关于点(
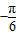 ,0)对称;
,0)对称;④y=f(x)的图象关于直线x=-
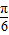 对称;
对称;其中正确命题的序号是( )
A.①②
B.②③
C.①③
D.②④
【答案】分析:分别利用三角函数的图象和性质进行判断即可.
解答:解:①由f(x1)=f(x2)=0,得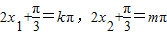 ,
,
所以2x1-2x2=(k-m)π,即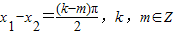 ,所以①错误.
,所以①错误.
②f(x)=4sin(2x+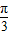 )=4cos(
)=4cos(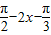 )=4cos(2x-
)=4cos(2x-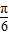 ),所以②正确.
),所以②正确.
③因为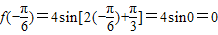 ,所以f(x)的图象关于点(
,所以f(x)的图象关于点(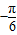 ,0)对称,所以③正确,④不正确.
,0)对称,所以③正确,④不正确.
故选B.
点评:本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的性质,综合性较强.
解答:解:①由f(x1)=f(x2)=0,得
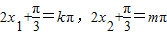 ,
,所以2x1-2x2=(k-m)π,即
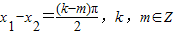 ,所以①错误.
,所以①错误.②f(x)=4sin(2x+
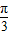 )=4cos(
)=4cos(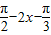 )=4cos(2x-
)=4cos(2x-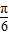 ),所以②正确.
),所以②正确.③因为
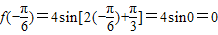 ,所以f(x)的图象关于点(
,所以f(x)的图象关于点(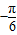 ,0)对称,所以③正确,④不正确.
,0)对称,所以③正确,④不正确.故选B.
点评:本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的性质,综合性较强.

练习册系列答案
相关题目
 )(
)( ),有下列命题:
),有下列命题: 可得
可得 必是
必是 的整数倍;
的整数倍;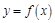 的表达式可改写为
的表达式可改写为 ;
; 对称;
对称; 对称.
对称.