题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{(2a-1)x+7a-2,x<1}\\{-a{x}^{2}-1,x≥1}\end{array}\right.$在(-∞,+∞)上单调递减,则实数a的取值范围[$\frac{1}{5}$,$\frac{1}{2}$).分析 根据分段函数单调性的性质进行求解即可.
解答 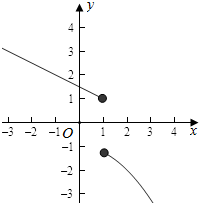 解:∵f(x)在(-∞,+∞)上单调递减,
解:∵f(x)在(-∞,+∞)上单调递减,
∴当x≥1和x<1时,分别单调递减,
即当x≥1时,满足-a<0,即a>0,
当x<1时,满足2a-1<0,即a<$\frac{1}{2}$,
同时满足2a-1+7a-2≥-a-1,
即10a≥2,得a≥$\frac{2}{10}$=$\frac{1}{5}$,
综上$\left\{\begin{array}{l}{a>0}\\{a<\frac{1}{2}}\\{a≥\frac{1}{5}}\end{array}\right.$,解得$\frac{1}{5}$≤a<$\frac{1}{2}$,
故实数a的取值范围是[$\frac{1}{5}$,$\frac{1}{2}$),
故答案为:[$\frac{1}{5}$,$\frac{1}{2}$)
点评 本题主要考查函数单调性的应用,根据分段函数单调性的性质是解决本题的关键.注意端点处的函数值的关系.

练习册系列答案
相关题目
18.已知映射f1:P→Q是从P到Q的函数,则P,Q的元素( )
| A. | 可以是点 | B. | 必须是实数 | C. | 可以是方程 | D. | 可以是三角形 |
15.已知a,b是两条不同的直线.α,β,γ是三个不重合的平面,则下列命题为真命题的是( )
| A. | 若a∥α,α⊥β,则a⊥β | |
| B. | 若a,b与α所成角相等,则a∥b | |
| C. | 若α⊥β,γ⊥β,则α∥γ | |
| D. | 若a,b为异面直线,a?α,a∥β,b?β,b∥α,则α∥β |
 PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.