题目内容
设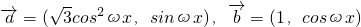 (其中ω>0),已知
(其中ω>0),已知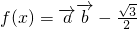 且f(x)最小正周期为2π
且f(x)最小正周期为2π
(1)求ω的值及y=f(x)的表达式;
(2)设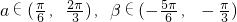 ,
,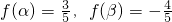 求cos(α-β)的值.
求cos(α-β)的值.
解:(1)∵已知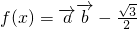 =
= cos2ωx+sinωx•cosωx-
cos2ωx+sinωx•cosωx- =
= sin2ωx+
sin2ωx+ cosωx=sin(2ωx+
cosωx=sin(2ωx+ ).
).
∵ω>0,T=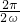 =2π,ω=
=2π,ω= ,
,
∴f(x)=sin(x+ ).
).
(2)∵f(α)= ,∴sin(α+
,∴sin(α+ )=
)= .
.
∵α∈( ,
, ),∴α+
),∴α+ ∈(
∈( ,π),cos(α+
,π),cos(α+ )=-
)=- .
.
再由f(β)=- ,可得sin(β+
,可得sin(β+ )=-
)=- .再由β∈(-
.再由β∈(- ,-
,- ),可得β+
),可得β+ ∈(-
∈(- ,0),
,0),
∴cos(β+ )=
)= .
.
∴cos(α-β)=cos[(α+ )-(β+
)-(β+ )]=cos(α+
)]=cos(α+ )cos(β+
)cos(β+ )-sin(α+
)-sin(α+ )•sin(β+
)•sin(β+ )=(-
)=(- )•(
)•(  )+(
)+(  )•(-
)•(- )=-
)=- .
.
分析:(1)利用三角函数的恒等变换化简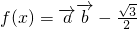 的解析式为 sin(2ωx+
的解析式为 sin(2ωx+ ),再由ω>0,T=
),再由ω>0,T=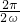 =2π,求得ω的值,即可求得f(x)的解析式.
=2π,求得ω的值,即可求得f(x)的解析式.
(2)根据角的范围以及同角三角函数的基本关系求出cos(α+ )、cos(β+
)、cos(β+ ),由cos(α-β)=cos[(α+
),由cos(α-β)=cos[(α+ )-(β+
)-(β+ )]利用两角和差的余弦公式求出结果.
)]利用两角和差的余弦公式求出结果.
点评:本题主要考查三角函数的恒等变换及化简求值,同角三角函数的基本关系,两角和差的余弦公式的应用,两个向量的数量积的定义,属于中档题.
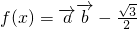 =
= cos2ωx+sinωx•cosωx-
cos2ωx+sinωx•cosωx- =
= sin2ωx+
sin2ωx+ cosωx=sin(2ωx+
cosωx=sin(2ωx+ ).
).∵ω>0,T=
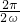 =2π,ω=
=2π,ω= ,
,∴f(x)=sin(x+
 ).
).(2)∵f(α)=
 ,∴sin(α+
,∴sin(α+ )=
)= .
.∵α∈(
 ,
, ),∴α+
),∴α+ ∈(
∈( ,π),cos(α+
,π),cos(α+ )=-
)=- .
.再由f(β)=-
 ,可得sin(β+
,可得sin(β+ )=-
)=- .再由β∈(-
.再由β∈(- ,-
,- ),可得β+
),可得β+ ∈(-
∈(- ,0),
,0),∴cos(β+
 )=
)= .
.∴cos(α-β)=cos[(α+
 )-(β+
)-(β+ )]=cos(α+
)]=cos(α+ )cos(β+
)cos(β+ )-sin(α+
)-sin(α+ )•sin(β+
)•sin(β+ )=(-
)=(- )•(
)•(  )+(
)+(  )•(-
)•(- )=-
)=- .
.分析:(1)利用三角函数的恒等变换化简
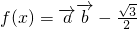 的解析式为 sin(2ωx+
的解析式为 sin(2ωx+ ),再由ω>0,T=
),再由ω>0,T=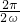 =2π,求得ω的值,即可求得f(x)的解析式.
=2π,求得ω的值,即可求得f(x)的解析式.(2)根据角的范围以及同角三角函数的基本关系求出cos(α+
 )、cos(β+
)、cos(β+ ),由cos(α-β)=cos[(α+
),由cos(α-β)=cos[(α+ )-(β+
)-(β+ )]利用两角和差的余弦公式求出结果.
)]利用两角和差的余弦公式求出结果.点评:本题主要考查三角函数的恒等变换及化简求值,同角三角函数的基本关系,两角和差的余弦公式的应用,两个向量的数量积的定义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目