Question

【题目】已知函数．

（1）若关于的方程只有一个实数解，求实数的取值范围；

（2）若当时，不等式恒成立，求实数的取值范围；

（3）探究函数在区间上的最大值（直接写出结果，不需给出演算步骤）．

Answer 1

【答案】（1）（2）（3）当时，在上的最大值为；

当时，在上的最大值为；

当时，在上的最大值为0.

【解析】

试题（1）方程，即，变形得，

显然，已是该方程的根，从而欲使原方程只有一解，

即要求方程有且仅有一个等于1的解或无解，

结合图形得. ……4分

（2）不等式对恒成立，即（*）对恒成立，

①当时，（*）显然成立，此时；

②当时，（*）可变形为，令

因为当时，，当时，，

所以，故此时.

综合①②，得所求实数的取值范围是. ……8分

（3）因为=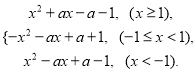……10分

①当时，结合图形可知在上递减，在上递增，

且，经比较，此时在上的最大值为.

②当时，结合图形可知在，上递减，

在，上递增，且，，

经比较，知此时在上的最大值为.

③当时，结合图形可知在，上递减，

在，上递增，且，，

经比较，知此时在上的最大值为.

④当时，结合图形可知在，上递减，

在，上递增，且,，

经比较，知此时在上的最大值为.

当时，结合图形可知在上递减，在上递增，

故此时在上的最大值为.

综上所述，当时，在上的最大值为；

当时，在上的最大值为；

当时，在上的最大值为0. ……15分