题目内容
如图所示,正方体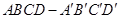 的棱长为1,
的棱长为1, 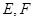 分别是棱
分别是棱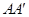 ,
,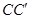 的中点,过直线
的中点,过直线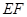 的平面分别与棱
的平面分别与棱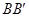 、
、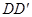 交于
交于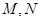 ,设
,设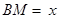 ,
,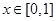 ,给出以下四个命题:
,给出以下四个命题: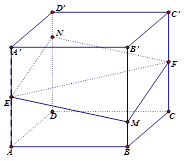
①平面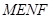
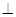 平面
平面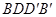 ;
;
②当且仅当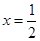 时,四边形
时,四边形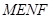 的面积最小;
的面积最小;
③四边形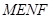 周长
周长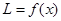 ,
,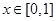 是单调函数;
是单调函数;
④四棱锥 的体积
的体积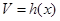 为常函数;
为常函数;
以上命题中真命题的序号为 。
①②④
解析试题分析:①连结 ,则由正方体的性质可知,
,则由正方体的性质可知, 平面
平面 ,所以平面
,所以平面 平面
平面 ,所以①正确;②连结
,所以①正确;②连结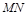 ,因为
,因为 平面
平面 ,所以
,所以 ,四边形
,四边形 的对角线
的对角线 是固定的,所以要使面积最小,则只需
是固定的,所以要使面积最小,则只需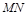 的长度最小即可,此时当
的长度最小即可,此时当 为棱的中点时,即
为棱的中点时,即 时,此时
时,此时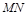 长度最小,对应四边形
长度最小,对应四边形 的面积最小.所以②正确;③因为
的面积最小.所以②正确;③因为 ,所以四边形
,所以四边形 是菱形.当
是菱形.当 时,
时, 的长度由大变小.当
的长度由大变小.当 时,
时, 的长度由小变大.所以函数
的长度由小变大.所以函数 不单调.所以③错误;④连结
不单调.所以③错误;④连结 则四棱锥分割为两个小三棱锥,它们以
则四棱锥分割为两个小三棱锥,它们以 为底,以
为底,以 分别为顶点的两个小棱锥.因为
分别为顶点的两个小棱锥.因为 的面积是个常数,
的面积是个常数, 到平面
到平面 的距离是个常数,所以四棱锥
的距离是个常数,所以四棱锥 的体积
的体积 为常函数,所以④正确.所以选C.
为常函数,所以④正确.所以选C.
考点:1、空间点线面位置关系;2、空间几何体面积与体积的计算.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
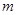 、
、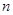 表示不同的直线,
表示不同的直线,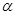 ,
,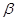 ,
,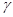 表示不同的平面,则下列四个命题正确的是 .
表示不同的平面,则下列四个命题正确的是 .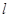 ,且
,且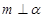 ,则
,则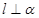 ;②若
;②若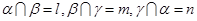 ,则
,则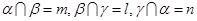 ,且
,且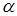 和
和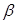 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题: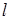 与
与 的底面是边长为
的底面是边长为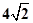 的正方形,侧棱长都等于
的正方形,侧棱长都等于 ,则经过该棱锥五个顶点的球面面积为__________.
,则经过该棱锥五个顶点的球面面积为__________.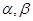 是两个互相垂直的平面,
是两个互相垂直的平面, 是一对异面直线,下列五个结论:
是一对异面直线,下列五个结论: ,
, (2)
(2)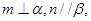 (3)
(3)
 (5)
(5) 。其中能得到
。其中能得到 的结论有 (把所有满足条件的序号都填上)
的结论有 (把所有满足条件的序号都填上) 及其三视图中的主视图和左视图如图9所示,则棱
及其三视图中的主视图和左视图如图9所示,则棱 的长为_________.
的长为_________.
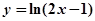 上的点到直线
上的点到直线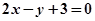 的最短距离是____________
的最短距离是____________ 的棱线长为1,线段
的棱线长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则三棱锥
,则三棱锥 的体积为
的体积为