题目内容
已知数列{an}中,
 Sn为该数列的前n项和,且Sn+1=an(1-an+1)+Sn.
Sn为该数列的前n项和,且Sn+1=an(1-an+1)+Sn.
(1)求数列{an}的通项公式;
(2)若不等式 对一切正整数n都成立,求正整数a的最大值,并证明结论.
对一切正整数n都成立,求正整数a的最大值,并证明结论.
解:(1)依题意作图如下:

∵图中x轴下方的等腰直角三角形与x轴上方、直线x=4及直线y=x-2组成的等腰直角三角形全等,
∴a1=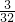
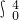
 dx=
dx=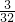 ×
×
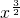 |
|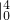 =
= ,
,
∵Sn+1=an(1-an+1)+Sn,
∴an+1=an-an•an+1,
∴ -
- =1,又a1=
=1,又a1= ,故
,故 =2,
=2,
,∴{ }是首项为2,公差为1的等差数列,
}是首项为2,公差为1的等差数列,
∴ =2+(n-1)×1=n+1,
=2+(n-1)×1=n+1,
.∴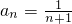 .
.
(2)当n=1时,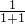 +
+ +
+ >
> ,即
,即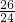 >
> ,
,
所以a<26,而a是正整数,
所以取a=25,下面用数学归纳法证明: +
+ +…+
+…+ >
>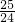 .
.
(1)当n=1时,已证;
(2)假设当n=k时,不等式成立,即 +
+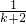 +…+
+…+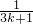 >
>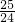 .
.
则当n=k+1时,
有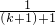 +
+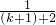 +…+
+…+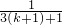
= +
+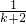 +…+
+…+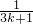 +
+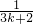 +
+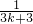 +
+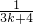 -
-
>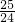 +[
+[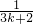 +
+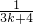 -
-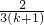 ].
].
因为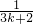 +
+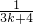 =
=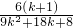 >
>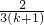 ,
,
所以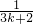 +
+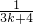 -
-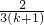 >0.
>0.
所以当n=k+1时不等式也成立.
由(1)(2)知,对一切正整数n,都有: +
+ +…+
+…+ >
>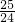 .
.
所以a的最大值等于25.
分析:(1)利用定积分可求得a1= ,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;
,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;
(2)当n=1时,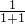 +
+ +
+ =
=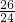 >
> ,于是a<26,据题意取a=25,用数学归纳法证明:
,于是a<26,据题意取a=25,用数学归纳法证明: +
+ +…+
+…+ >
>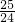 即可.
即可.
点评:本题考查数列递推式,考查数学归纳法,利用定积分求得a1= 是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题.
是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题.

∵图中x轴下方的等腰直角三角形与x轴上方、直线x=4及直线y=x-2组成的等腰直角三角形全等,
∴a1=
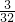
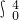
 dx=
dx=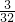 ×
×
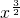 |
|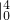 =
= ,
,∵Sn+1=an(1-an+1)+Sn,
∴an+1=an-an•an+1,
∴
 -
- =1,又a1=
=1,又a1= ,故
,故 =2,
=2,,∴{
 }是首项为2,公差为1的等差数列,
}是首项为2,公差为1的等差数列,∴
 =2+(n-1)×1=n+1,
=2+(n-1)×1=n+1,.∴
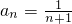 .
.(2)当n=1时,
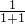 +
+ +
+ >
> ,即
,即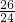 >
> ,
,所以a<26,而a是正整数,
所以取a=25,下面用数学归纳法证明:
 +
+ +…+
+…+ >
>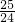 .
.(1)当n=1时,已证;
(2)假设当n=k时,不等式成立,即
 +
+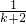 +…+
+…+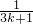 >
>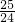 .
.则当n=k+1时,
有
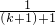 +
+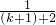 +…+
+…+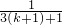
=
 +
+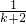 +…+
+…+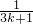 +
+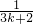 +
+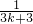 +
+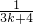 -
-
>
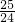 +[
+[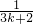 +
+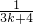 -
-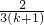 ].
].因为
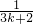 +
+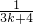 =
=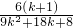 >
>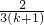 ,
,所以
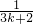 +
+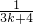 -
-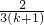 >0.
>0.所以当n=k+1时不等式也成立.
由(1)(2)知,对一切正整数n,都有:
 +
+ +…+
+…+ >
>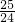 .
.所以a的最大值等于25.
分析:(1)利用定积分可求得a1=
 ,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;
,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;(2)当n=1时,
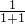 +
+ +
+ =
=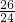 >
> ,于是a<26,据题意取a=25,用数学归纳法证明:
,于是a<26,据题意取a=25,用数学归纳法证明: +
+ +…+
+…+ >
>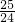 即可.
即可.点评:本题考查数列递推式,考查数学归纳法,利用定积分求得a1=
 是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题.
是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题. 
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|