题目内容
(12分)已知函数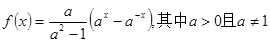
(1)判断函数的奇偶性和单调性;
(2)当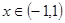 时,有
时,有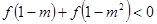 ,求
,求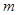 的取值范围.
的取值范围.
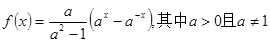
(1)判断函数的奇偶性和单调性;
(2)当
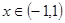 时,有
时,有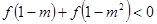 ,求
,求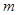 的取值范围.
的取值范围. 解:(1)奇函数. 增函数.(2)
增函数.(2) .
.
 增函数.(2)
增函数.(2) .
.本题主要考查了证明函数奇偶性的方法,利用函数单调性的定义证明函数单调性的方法步骤,代数变形能力和逻辑推理能力。
(1)先确定函数的定义域,再利用奇函数的定义,证明函数f(x)=-f(-x),从而函数为奇函数;
(2)因为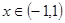 所以
所以 即
即 ,由(1)得
,由(1)得 为奇函数且是R上的增函数,进而解得。
为奇函数且是R上的增函数,进而解得。
解:(1)函数的定义域为R , 所以
所以 为奇函数.
为奇函数.
当 时
时 ,
, 单调递减所以
单调递减所以 单调递增;
单调递增;
当 时
时 ,
, 单调递增所以
单调递增所以 单调递增.
单调递增.
总上所述函数 增函数.
增函数.
(2)因为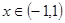 所以
所以 即
即 ,由(1)得
,由(1)得 为奇函数且是R上的增函数所以由
为奇函数且是R上的增函数所以由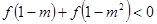 得
得 
即
解得 综上得
综上得 所以
所以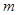 的取值范围是
的取值范围是 .
.
(1)先确定函数的定义域,再利用奇函数的定义,证明函数f(x)=-f(-x),从而函数为奇函数;
(2)因为
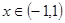 所以
所以 即
即 ,由(1)得
,由(1)得 为奇函数且是R上的增函数,进而解得。
为奇函数且是R上的增函数,进而解得。解:(1)函数的定义域为R ,
 所以
所以 为奇函数.
为奇函数.当
 时
时 ,
, 单调递减所以
单调递减所以 单调递增;
单调递增; 当
 时
时 ,
, 单调递增所以
单调递增所以 单调递增.
单调递增.总上所述函数
 增函数.
增函数.(2)因为
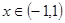 所以
所以 即
即 ,由(1)得
,由(1)得 为奇函数且是R上的增函数所以由
为奇函数且是R上的增函数所以由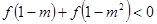 得
得 
即

解得
 综上得
综上得 所以
所以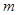 的取值范围是
的取值范围是 .
.
练习册系列答案
相关题目
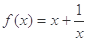
 在
在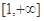 上是增函数;
上是增函数;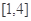 上的最大值及最小值。
上的最大值及最小值。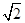 ]上的最小值.
]上的最小值.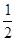 )=0,则不等式f(log4x)>0的解集是______________.
)=0,则不等式f(log4x)>0的解集是______________.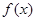 在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则函数
在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则函数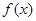 的定义域为
的定义域为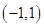 ,且同时满足下列条件:
,且同时满足下列条件: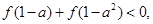 求
求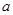 的取值范围。
的取值范围。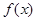 =
=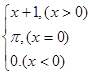 求
求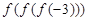 的值。
的值。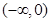 上是增函数的是( )
上是增函数的是( )