题目内容
已知圆M：（x+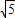
）2+y2=36，定点N（
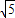，0），点P为圆M上的动点，点Q在NP上，点G在MP上，且满足
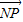=2
，
•
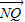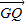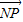=0．（I）求点G的轨迹C的方程；
（II）点F（x，y）在轨迹C上，求2x2+y的最大值与最小值．
【答案】分析：（I）由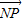
=2
，
•
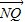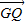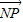=0，知Q为PN的中点且GQ⊥PN，∴GQ为PN的中垂线，∴|PG|=|GN|，∴|GN|+|GM|=|MP|=6，故G点的轨迹是以M、N为焦点的椭圆，从而可求方程；（Ⅱ）易知-2≤y≤2，从而转化为二次函数求最值．
解答：解：（Ⅰ）由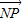
=2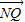
，
•
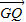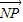=0，知Q为PN的中点且GQ⊥PN，∴GQ为PN的中垂线，∴|PG|=|GN|
∴|GN|+|GM|=|MP|=6，故G点的轨迹是以M、N为焦点的椭圆，其长半轴长a=3，半焦距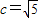
，∴短半轴长b=2，
∴点G的轨迹方程是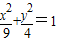
（Ⅱ）易知-2≤y≤2，当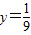
时，2x2+y有最大值18
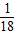，当y=-2时，2x2+y有最小值为-2
点评：本题主要考查椭圆的定义，解题的关键是将问题等价转化为符合椭圆的定义，（Ⅱ）的关键是从转化为二次函数求最值．
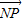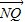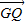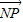=2，•=0，知Q为PN的中点且GQ⊥PN，∴GQ为PN的中垂线，∴|PG|=|GN|，∴|GN|+|GM|=|MP|=6，故G点的轨迹是以M、N为焦点的椭圆，从而可求方程；（Ⅱ）易知-2≤y≤2，从而转化为二次函数求最值．解答：解：（Ⅰ）由
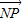=2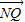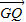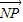，•=0，知Q为PN的中点且GQ⊥PN，∴GQ为PN的中垂线，∴|PG|=|GN|∴|GN|+|GM|=|MP|=6，故G点的轨迹是以M、N为焦点的椭圆，其长半轴长a=3，半焦距
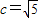，∴短半轴长b=2，∴点G的轨迹方程是
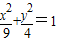
（Ⅱ）易知-2≤y≤2，当
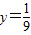时，2x2+y有最大值18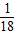，当y=-2时，2x2+y有最小值为-2点评：本题主要考查椭圆的定义，解题的关键是将问题等价转化为符合椭圆的定义，（Ⅱ）的关键是从转化为二次函数求最值．
练习册系列答案
相关题目
）2+y2=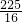
的圆心为M，圆N：（x-
）2+y2=36，定点N（
，0），点P为圆M上的动点，点Q在NP上，点G在MP上，且满足
。
是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由。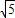
）2+y2=36，定点N（
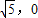），点P为圆M上的动点，点G在MP上，且满足|GP|=|GN|
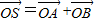，是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由．
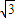）2+y2=
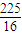的圆心为M，圆N：（x-
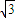）2+y2=的圆心为N，一动圆与圆M内切，与圆N外切．
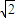）2+y2=r2=r2（r＞0）．若椭圆C：
+
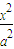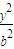=1（a＞b＞0）的右顶点为圆M的圆心，离心率为
．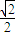