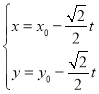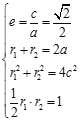Question

【题目】已知椭圆C：（）的焦距为，且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于、，且在椭圆C上存在点M，使得：（其中O为坐标原点），则称直线l具有性质H.

（1）求椭圆C的方程；

（2）若直线l垂直于x轴，且具有性质H，求直线l的方程；

（3）求证：在椭圆C上不存在三个不同的点P、Q、R，使得直线、、都具有性质H.

Answer 1

【答案】（1）（2）；（3）证明见解析；

【解析】

(1)根据正三角形中的长度关系列出的关系求解即可.

(2) 设直线,再求得满足的关系式,进而代入化简求解即可.

(3)假设存在椭圆C上不存在三个不同的点P、Q、R满足条件,再将对应的点坐标代入椭圆方程,分情况讨论得出矛盾即可.

(1),所以,

又右焦点F与短轴的两个端点组成一个正三角形,所以,

因为,

解得：,,

所以,椭圆方程为：

(2)设直线,则,

其中满足：,,

设,

∵（其中O为坐标原点）,

∴,

∵点在椭圆上,

∴,

∴,

∴,

∴直线的方程为或.

(3) 证明：假设在椭圆上存在三个不同的点,

使得直线都具有性质,

∵直线具有性质,

∴在椭圆上存在点M,使得：,

设,则,,

∵点在椭圆上,∴,

又∵,,代入化简得,①

同理：②, ,③

1)若中至少一个为0,不妨设,则,

由①③得,即为长轴的两个端点,则②不成立,矛盾。

2)若均不为0,则由①②③得,矛盾。

∵在椭圆C上不存在三个不同的点P、Q、R,使得直线、、都具有性质H.