Question

【题目】如图，在平面四边形中，和都是等腰直角三角形且，正方形的边.

（1）求证：平面；

（2）求二面角的余弦值.

Answer 1

【答案】(1)证明见解析；(2).

【解析】试题分析：

（1）由线面垂直的判断定理可得平面则由平面几何知识可得，据此有平面．

（2）由题意可知AD，AB，AE两两垂直．建立空间直角坐标系，设AB=1，据此可得平面BDF的一个法向量为，取平面ABD的一个法向量为，则二面角的余弦值为．

试题解析：

（1）正方形中，

又且，所以

又

因为和都是等腰直角三角形，

所以，

即，且，

所以．

（2）因为△ABE是等腰直角三角形，所以，

又因为，所以，

即AD，AB，AE两两垂直．建立如图所示空间直角坐标系，

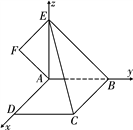
设AB=1，则AE=1，，

，

设平面BDF的一个法向量为，

可得，

取平面ABD的一个法向量为，

则，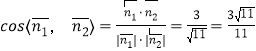

故二面角的余弦值为．