题目内容
设f（x）=3ax2+2bx+c，若a+b+c=0，f（0）＞0，f（1）＞0，
求证（1）a＞0且
；
（2）方程f（x）=0在（0，1）内有实根；
求证（1）a＞0且
；（2）方程f（x）=0在（0，1）内有实根；
解：（1）因为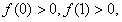
所以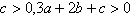
由条件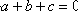
，消去b，得
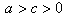
由条件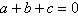
，消去c，得
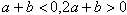
故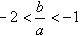
。
（2）抛物线f（x）=3ax2+2bx+c的顶点坐标为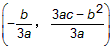
在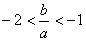
的两边乘以-
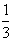得
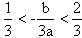
又因为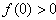
，
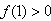
而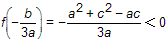
所以方程f（x）=0在区间（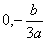
）与（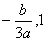
）内分别有一根
故方程f（x）=0在（0，1）内有两个实根。
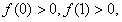
所以
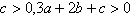
由条件
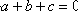，消去b，得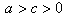由条件
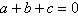，消去c，得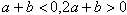故
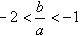。（2）抛物线f（x）=3ax2+2bx+c的顶点坐标为
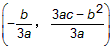
在
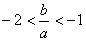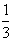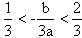
的两边乘以-得又因为
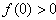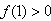
，而
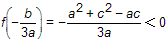
所以方程f（x）=0在区间（
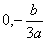）与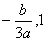（）内分别有一根故方程f（x）=0在（0，1）内有两个实根。
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目