题目内容
已知平面向量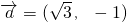 ,
,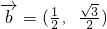 .
.
(1)求证: ;
;
(2)设 ,
, (其中x≠0),若
(其中x≠0),若 ,试求函数关系式y=f(x),并解不等式f(x)>7.
,试求函数关系式y=f(x),并解不等式f(x)>7.
解:(1)∵ ∴
∴ ;
;
(2)由 得,-4y+x(x-3)=0,所以
得,-4y+x(x-3)=0,所以  ;
;
由 变形得:x2-3x-28>0,解得x>7或x<-4.
变形得:x2-3x-28>0,解得x>7或x<-4.
所以不等式的解集是(-∞,-4)∪(7,+∞)
分析:(1)直接根据向量的数量积公式 =x1x2+y1y2进行求解,
=x1x2+y1y2进行求解, 可得求证:
可得求证: ;
;
(2)根据由 得x和y的关系,然后根据f(x)>7建立不等式,解之即可.
得x和y的关系,然后根据f(x)>7建立不等式,解之即可.
点评:本题主要考查了向量的数量积,同时考查了不等式的解法,属于中档题.
 ∴
∴ ;
;(2)由
 得,-4y+x(x-3)=0,所以
得,-4y+x(x-3)=0,所以  ;
;由
 变形得:x2-3x-28>0,解得x>7或x<-4.
变形得:x2-3x-28>0,解得x>7或x<-4.所以不等式的解集是(-∞,-4)∪(7,+∞)
分析:(1)直接根据向量的数量积公式
 =x1x2+y1y2进行求解,
=x1x2+y1y2进行求解, 可得求证:
可得求证: ;
;(2)根据由
 得x和y的关系,然后根据f(x)>7建立不等式,解之即可.
得x和y的关系,然后根据f(x)>7建立不等式,解之即可.点评:本题主要考查了向量的数量积,同时考查了不等式的解法,属于中档题.

练习册系列答案
相关题目
已知平面向量
=(3,1),
=(x,-3),
∥
,则x等于( )
| a |
| b |
| a |
| b |
| A、9 | B、1 | C、-1 | D、-9 |