题目内容
如果函数f(x)=logax•(logax-3a2-1)(a>0,a≠1)在区间[a,+∞)是增函数,那么实数a的取值范围是( )
A.(0,
| B.[
| C.(1,+∞) | D.(0,1) |
当a>1时,logax与logax-3a2-1两个因子都是增函数,且logax≥1,故只需logax-3a2-1>0即可,即logax>3a2+1在区间[a,+∞)恒成立,此不可能
当0<a<1时,logax与logax-3a2-1两个因子都是减函数,且logax≤1,故只需logax-3a2-1<0即可,即logax<3a2+1在区间[a,+∞)恒成立,显然成立
综上知实数a的取值范围是(0,1)
故选D
当0<a<1时,logax与logax-3a2-1两个因子都是减函数,且logax≤1,故只需logax-3a2-1<0即可,即logax<3a2+1在区间[a,+∞)恒成立,显然成立
综上知实数a的取值范围是(0,1)
故选D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 旦(a>0)有如下的性质:在区间(0,
旦(a>0)有如下的性质:在区间(0, ]上单调递减,在[
]上单调递减,在[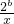 在(0,4]上单调递减,在[4,+∞)上单调递增,求常数b的值.
在(0,4]上单调递减,在[4,+∞)上单调递增,求常数b的值. 旦(a>0)有如下的性质:在区间(0,
旦(a>0)有如下的性质:在区间(0,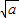 ]上单调递减,在[
]上单调递减,在[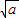 ,+∞)上单调递增.
,+∞)上单调递增.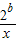 在(0,4]上单调递减,在[4,+∞)上单调递增,求常数b的值.
在(0,4]上单调递减,在[4,+∞)上单调递增,求常数b的值.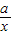 在x∈[l,2]的最大值.
在x∈[l,2]的最大值.