题目内容
设V是已知平面M上所有向量的集合,对于映射f:V→V,
∈V,记
的象为f(
).若映射f:V→V满足:对所有
,
∈V及任意实数λ,μ都有f(λ
+μ
)=λf(
)+μf(
),则f称为平面M上的线性变换.现有下列命题:
①设f是平面M上的线性变换,则f(
)=
②对
∈V设f(
)=2
,则f是平面M上的线性变换;
③若
是平面M上的单位向量,对
∈V设f(
)=
-
,则f是平面M上的线性变换;
④设f是平面M上的线性变换,
,
∈V,若
,
共线,则f(
),f(
)也共线.
其中真命题是______(写出所有真命题的序号)
| a |
| a |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
①设f是平面M上的线性变换,则f(
| 0 |
| 0 |
②对
| a |
| a |
| a |
③若
| e |
| a |
| a |
| a |
| e |
④设f是平面M上的线性变换,
| a |
| b |
| a |
| b |
| a |
| b |
其中真命题是______(写出所有真命题的序号)
令
=
=
,λ=μ=1,
由题有f(
)=2f(
)?f(
)=
,故①正确;
由题f(λ
+μ
)=2(λ
+μ
),
λf(
)+μf(
)=2λ
+2μ
)=2(λ
+μ
),
即f(λ
+μ
)=λf(
)+μf(
),故②正确;
由题f(λ
+μ
)=λ
+μ
-
,
λf(
)+μf(
)=λ
-
+μ
-
,,
即f(λ
+μ
≠λf(
)+μf(
),故③不正确;
由题
=λ
,f(
)=f(
-λ
)=f(
)-λf(
)
?f(
)=λf(
),
即f(
),f(
)也共线,故④正确;
故答案为:①②④
| a |
| b |
| 0 |
由题有f(
| 0 |
| 0 |
| 0 |
| 0 |
由题f(λ
| a |
| b |
| a |
| b |
λf(
| a |
| b |
| a |
| b |
| a |
| b |
即f(λ
| a |
| b |
| a |
| b |
由题f(λ
| a |
| b |
| a |
| b |
| e |
λf(
| a |
| b |
| a |
| e |
| b |
| e |
即f(λ
| a |
| b |
| a |
| b |
由题
| b |
| a |
| 0 |
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
即f(
| a |
| b |
故答案为:①②④

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 ,记
,记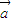 的象为
的象为 .若映射f:V→V满足:对所有
.若映射f:V→V满足:对所有 及任意实数λ,μ都有
及任意实数λ,μ都有 ,则f称为平面M上的线性变换.现有下列命题:
,则f称为平面M上的线性变换.现有下列命题:
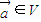 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换; 是平面M上的单位向量,对
是平面M上的单位向量,对 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换; ,若
,若 共线,则
共线,则 也共线.
也共线.